自然语言和单词的分布式表示(word embedding)
自然语言处理
我们平常使用的语言,如日语或英语,称为自然语言(natural language)。所谓自然语言处理(Natural Language Processing,NLP),顾名思义,就是处理自然语言的科学。简单地说,它是一种能够让计算机理解人类语言的技术。
搜索引擎和机器翻译就是两个比较好理解的例子,除此之外,还有问答系统、假名汉字转化(IME)、自动文本摘要和情感分析等,在我们身边已经使用了很多自然语言处理技术。
以下方法将探讨如何是计算机理解单词含义,并且得到单词的计算机表示(离散表示、向量表示、embedding)。
同义词词典
以英文为例,人工构建同义词的词典,使之形成图结构的单词网络。
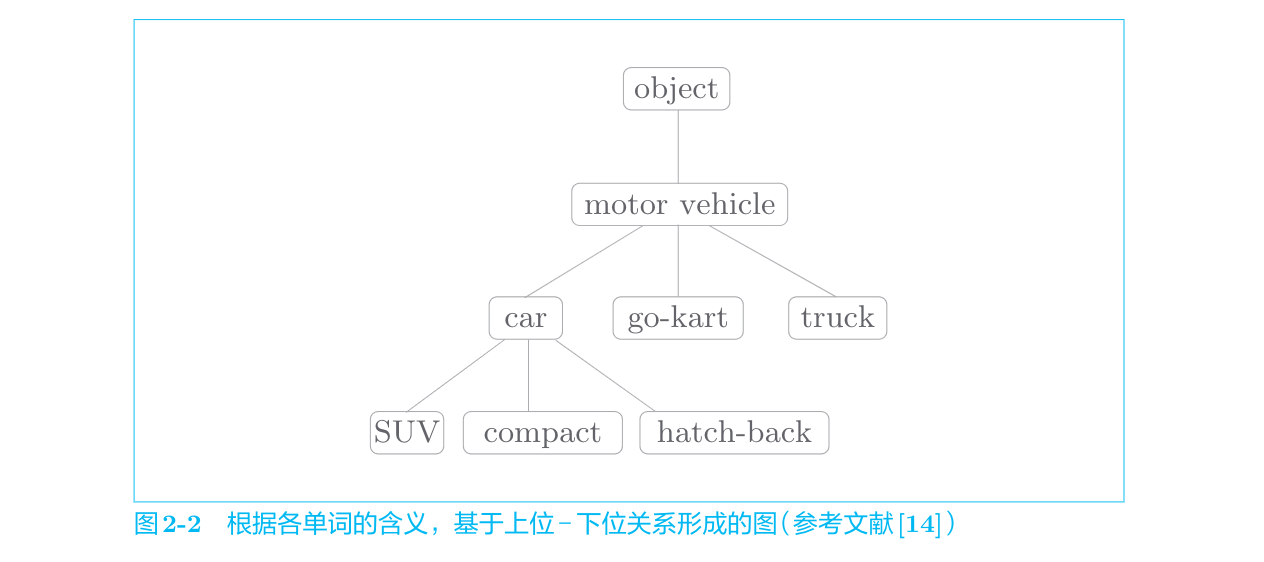
在自然语言处理领域,最著名的同义词词典是WordNet。使用WordNet,可以获得单词的近义词,或者利用单词网络。使用单词网络,可以计算单词之间的相似度。
这个方法存在很大的局限性:
- 难以顺应时代变化(更新缓慢)
- 人力成本高
- 无法表示单词的微妙差异(没有一个相似度量化指标)
基于计数的方法
语料库
从介绍基于计数的方法开始,我们将使用语料库(corpus)。简而言之,语料库就是大量的文本数据。不过,语料库并不是胡乱收集数据,一般收集的都是用于自然语言处理研究和应用的文本数据。
单词的分布式表示
世界上的颜色可以通过RGB(Red/Green/Blue)三原色分别存在多少来进行表示,将颜色表示为三维向量,且这种基于三原色的表示方式很紧凑,也更容易让人想象到具体是什么颜色。也就是说视觉上相似的颜色,在于rgb这个空间上的距离也是相近的。将这种方式类比到文字上,构建出紧凑合理的准确把握单词含义的向量表示。在自然语言处理领域,这称为分布式表示。
分布式假设
“某个单词的含义由它周围的单词形成”,称为分布式假设(distributional hypothesis)。
共现矩阵
设定一个固定的窗口大小,对一段文字进行统计,将每个单词在其窗口大小内的其他单词进行标注。
例如

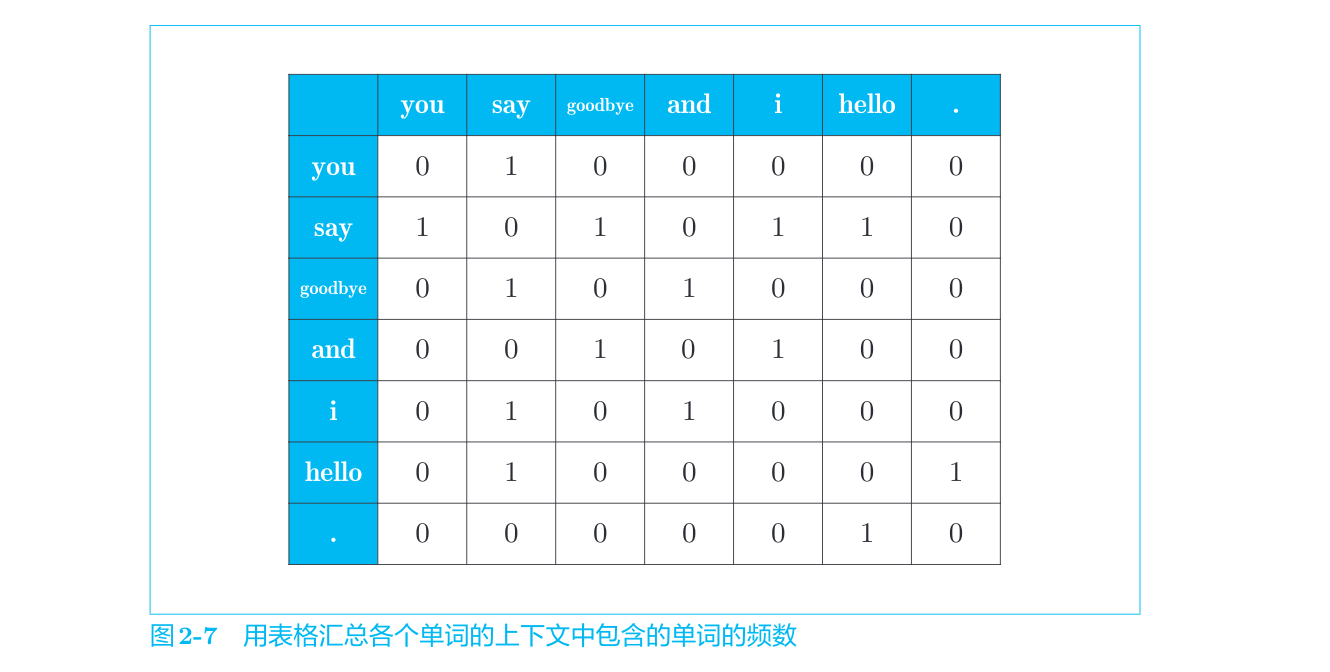
得到了每个单词对于其窗口大小内其他出现单词的统计,汇总得到一个矩阵,称为共现矩阵(co-occurence matrix)。
通过共现矩阵其实我们就已经得到了单词的向量表示的雏形,即根据分布式假设,将单词的意思抽象成该单词上下文内的词汇,而这个上下文向量距离较短的两对单词,说明这两个单词上下文中出现的单词是差不多的,因此得到这两个单词的意思是相近的。
向量间的相似度
测量向量间的相似度有很多方法,其中具有代表性的方法有向量内积或欧式距离等。虽然除此之外还有很多方法,但是在测量单词的向量表示的相似度方面,余弦相似度(cosine similarity)是很常用的。设有
在式(2.1)中,分子是向量内积,分母是各个向量的范数。范数表示向量的大小,这里计算的是L2范数(即向量各个元素的平方和的平方根)。式(2.1)的要点是先对向量进行正规化,再求它们的内积。
余弦相似度直观地表示了“两个向量在多大程度上指向同一方向”。两个向量完全指向相同的方向时,余弦相似度为1;完全指向相反的方向时,余弦相似度为−1。
基于计数的方法的改进
点互信息
上一节的共现矩阵的元素表示两个单词同时出现的次数。但是,这种“原始”的次数并不具备好的性质。在这种方法下一些常用词会和许多词汇产生极强的相关性,这并不是预期的结果,为了解决这种问题需要对常用词进行一些惩罚机制。
为了解决这一问题,可以使用点互信息(Pointwise Mutual Information,PMI)这一指标。对于随机变量x和y,它们的PMI定义如下:
其中,
自然语言的例子中,
降维
所谓降维(dimensionality reduction),顾名思义,就是减少向量维度。但是,并不是简单地减少,而是在尽量保留“重要信息”的基础上减少。如图2-8所示,我们要观察数据的分布,并发现重要的“轴”。
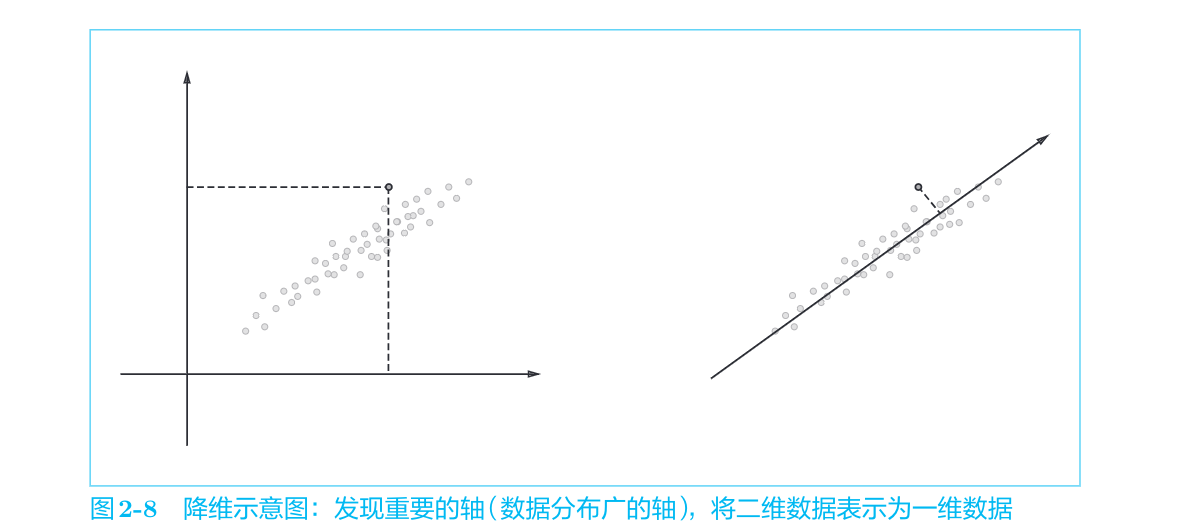
向量中的大多数元素为0的矩阵(或向量)称为稀疏矩阵(或稀疏向量)。这里的重点是,从稀疏向量中找出重要的轴,用更少的维度对其进行重新表示。结果,稀疏矩阵就会被转化为大多数元素均不为0的密集矩阵。这个密集矩阵就是我们想要的单词的分布式表示。
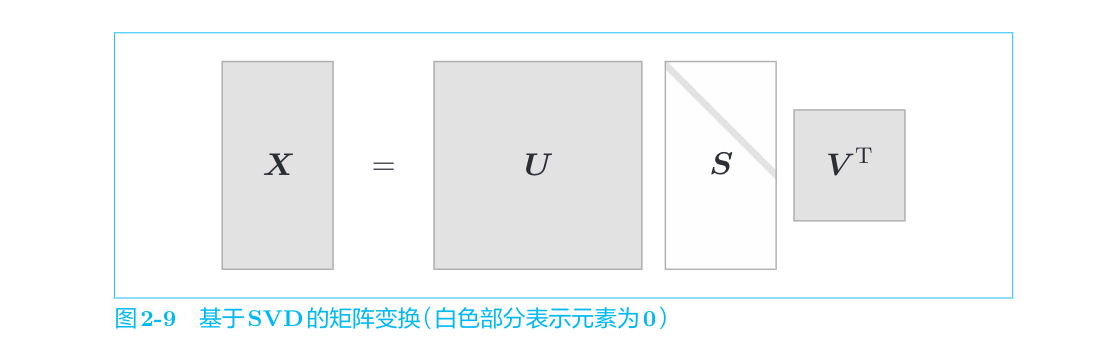
降维的方法有很多,这里我们使用奇异值分解(Singular Value Decomposition,SVD)。SVD将任意矩阵分解为3个矩阵的乘积,如下式所示:
SVD将任意的矩阵
word2vec
基于推理的方法和神经网络
用向量表示单词的研究中比较成功的方法大致可以分为两种:一种是基于计数的方法;另一种是基于推理的方法。虽然两者在获得单词含义的方法上差别很大,但是两者的背景都是分布式假设。
基于计数的方法的问题
基于计数的方法根据一个单词周围的单词的出现频数来表示该单词。具体来说,先生成所有单词的共现矩阵,再对这个矩阵进行SVD,以获得密集向量(单词的分布式表示)。但是,基于计数的方法在处理大规模语料库时会出现问题。
在现实世界中,语料库处理的单词数量非常大。比如,据说英文的词汇量超过100万个。如果词汇量超过100万个,那么使用基于计数的方法就需要生成一个100万×100万的庞大矩阵,但对如此庞大的矩阵执行SVD显然是不现实的。
基于计数的方法使用整个语料库的统计数据(共现矩阵和PPMI等 ),通过一次处理(SVD等)获得单词的分布式表示。而基于推理的方法使用神经网络,通常在mini-batch数据上进行学习。这意味着神经网络一次只需要看一部分学习数据(mini-batch),并反复更新权重。这种学习机制上的差异如图3-1所示。
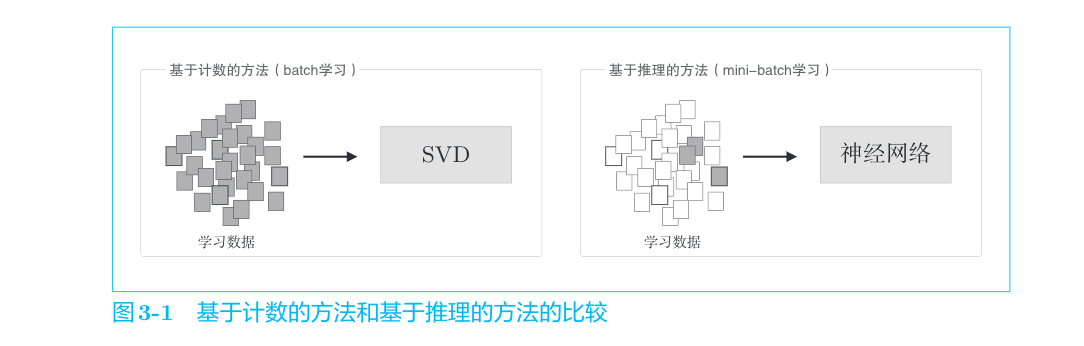
基于计数的方法一次性处理全部学习数据;反之,基于推理的方法使用部分学习数据逐步学习。这意味着,在词汇量很大的语料库中,即使SVD等的计算量太大导致计算机难以处理,神经网络也可以在部分数据上学习。并且,神经网络的学习可以使用多台机器、多个GPU并行执行,从而加速整个学习过程。在这方面,基于推理的方法更有优势。
基于推理的方法的概要
于推理的方法的主要操作是“推理”。如图3-2所示,当给出周围的单词(上下文)时,预测“?”处会出现什么单词,这就是推理。这种方法可以称为是无监督学习,因为所需要输入的数据是大量现存的语料,不需要人为标注,学习目标为预测输入语句下一个会出现的词。

解开图3-2中的推理问题并学习规律,就是基于推理的方法的主要任务。通过反复求解这些推理问题,可以学习到单词的出现模式。从“模型视角”出发,这个推理问题如图3-3所示。
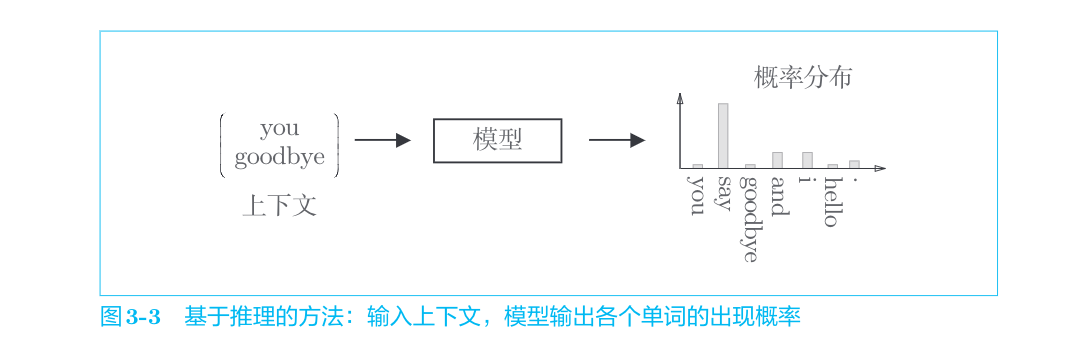
如图3-3所示,基于推理的方法引入了某种模型,我们将神经网络用于此模型。这个模型接收上下文信息作为输入,并输出(可能出现的)各个单词的出现概率。在这样的框架中,使用语料库来学习模型,使之能做出正确的预测。另外,作为模型学习的产物,我们得到了单词的分布式表示。这就是基于推理的方法的全貌。
也就是说在训练完这个模型同时,我们可以从某一层提取到单词的向量表示。
神经网络中单词的处理方法
要用神经网络处理单词,需要先将单词转化为固定长度的向量。对此,一种方式是将单词转换为one-hot表示(one-hot向量)。在one-hot表示中,只有一个元素是1,其他元素都是0。
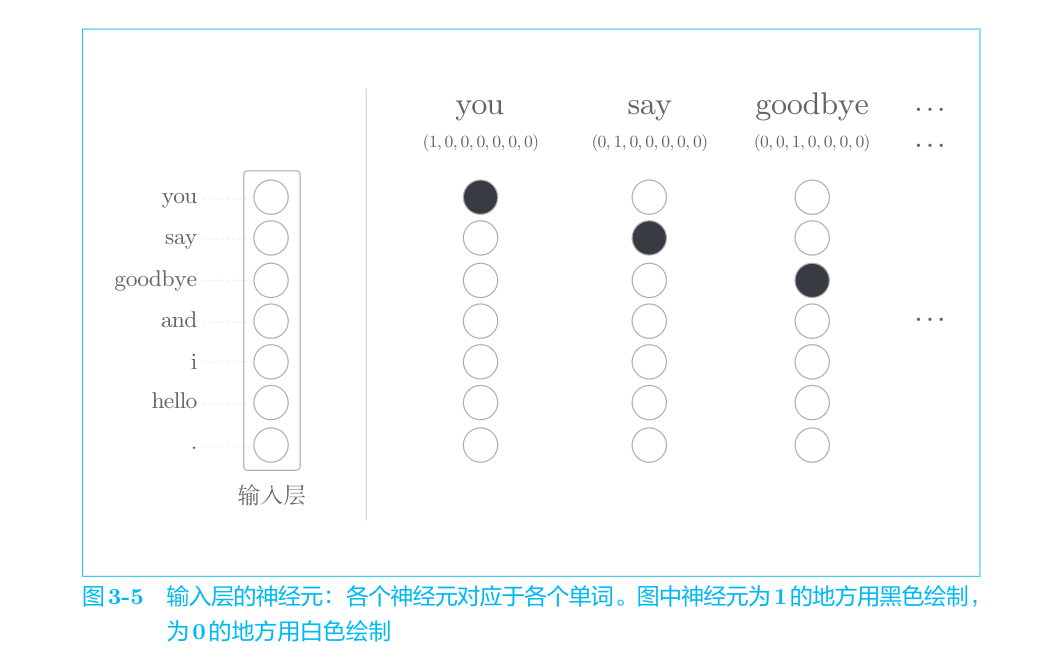
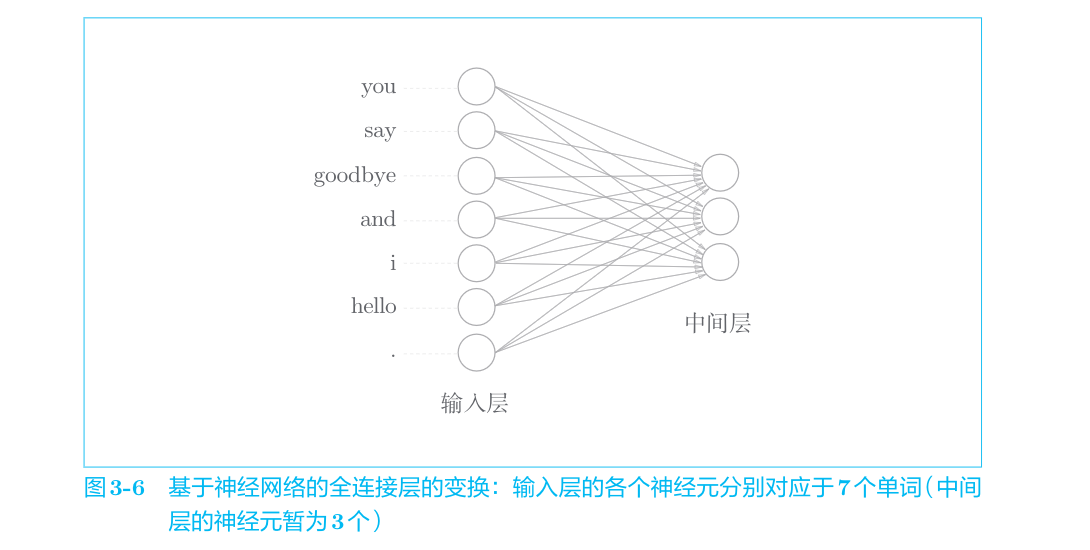
对于one-hot表示的某个单词,使用全连接层对其进行变换的情况如图3-6所示
CBOW模型的推理
CBOW模型是word2vec的一种,它有两个输入层,经过中间层到达输出层。这里,从输入层到中间层的变换由相同的全连接层(权重为
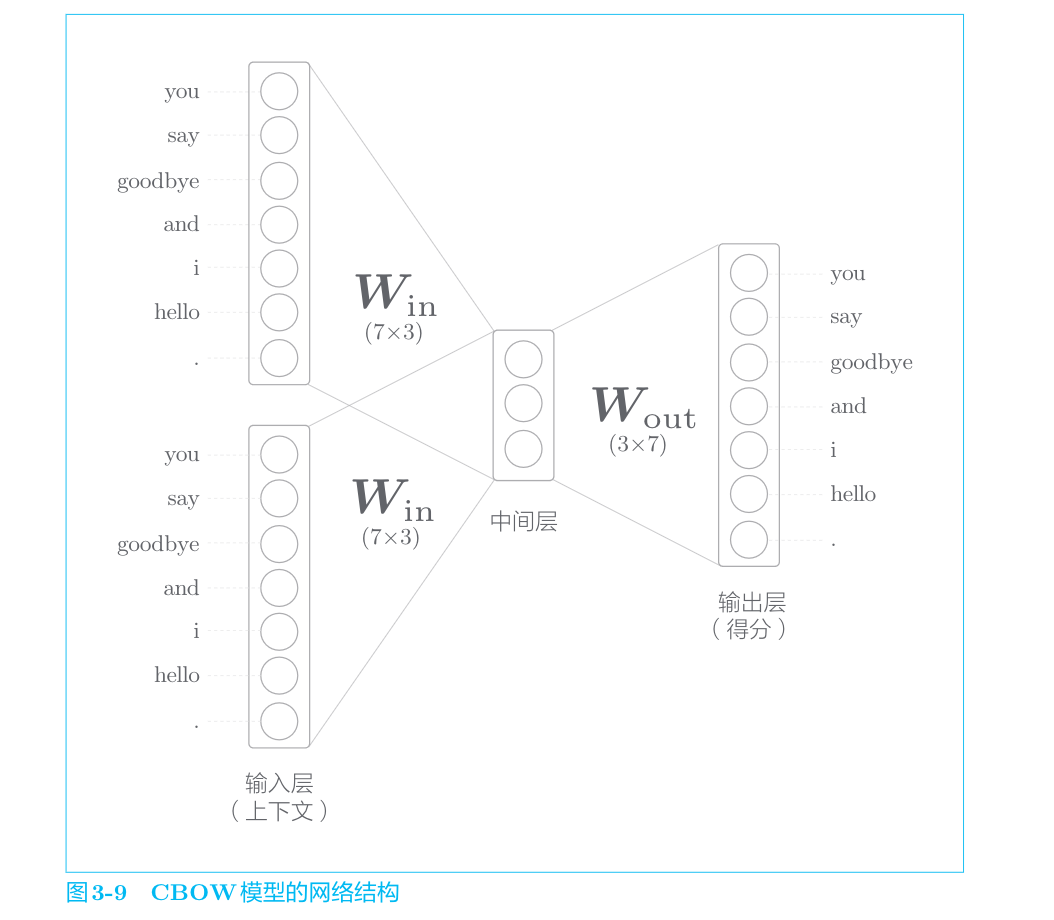
中间层的神经元是各个输入层经全连接层变换后得到的值的“平均”。就上面的例子而言,经全连接层变换后,第1个输入层转化为
最后是图3-9中的输出层,这个输出层有7个神经元。这里重要的是,这些神经元对应于各个单词。输出层的神经元是各个单词的得分,它的值越大,说明对应单词的出现概率就越高。得分是指在被解释为概率之前的值,对这些得分应用Softmax函数,就可以得到概率。
如图3-9所示,从输入层到中间层的变换由全连接层(权重是

中间层的神经元数量比输入层少这一点很重要。中间层需要将预测单词所需的信息压缩保存,从而产生密集的向量表示。这时,中间层被写入了我们人类无法解读的代码,这相当于“编码”工作。而从中间层的信息获得期望结果的过程则称为“解码”。这一过程将被编码的信息复原为我们可以理解的形式。
补充说明
有一个常见的误解,那就是基于推理的方法在准确度方面优于基于计数的方法。实际上,有研究表明,就单词相似性的定量评价而言,基于推理的方法和基于计数的方法难分上下。
使用word2vec获得的单词的分布式表示可以用来查找近似单词,但是单词的分布式表示的好处不仅仅在于此。在自然语言处理领域,单词的分布式表示之所以重要,原因就在于迁移学习(transfer learning)。迁移学习是指在某个领域学到的知识可以被应用于其他领域。
在解决自然语言处理任务时,一般不会使用word2vec从零开始学习单词的分布式表示,而是先在大规模语料库(Wikipedia、Google News等文本数据)上学习,然后将学习好的分布式表示应用于某个单独的任务。比如,在文本分类、文本聚类、词性标注和情感分析等自然语言处理任务中,第一步的单词向量化工作就可以使用学习好的单词的分布式表示。在几乎所有类型的自然语言处理任务中,单词的分布式表示都有很好的效果!
循环神经网络(Recurrent Neural Network,RNN)
概率和语言模型
概率视角下的word2vec
CBOW模型所做的事情就是从上下文(

用数学式来表示“当给定
CBOW模型对这一后验概率进行建模。这个后验概率表示“当给定

在仅将左侧2个单词作为上下文的情况下,CBOW模型输出的概率:
CBOW模型的损失函数可以写成
语言模型(概率分解)
语言模型(language model)给出了单词序列发生的概率。
我们使用数学式来表示语言模型。这里考虑由
使用后验概率可以将这个联合概率

Simple RNN
Recurrent Neural Network通常译为“循环神经网络”。另外,还有一种被称为Recursive Neural Network(递归神经网络)的网络。这个网络主要用于处理树结构的数据,和循环神经网络不是一个东西。
循环的神经网络
RNN的特征就在于拥有这样一个环路(或回路)。这个环路可以使数据不断循环。通过数据的循环,RNN一边记住过去的数据,一边更新到最新的数据。环路的设计使rnn拥有了记忆性,这与CBOW(bag of word)中的无序性差别很大。
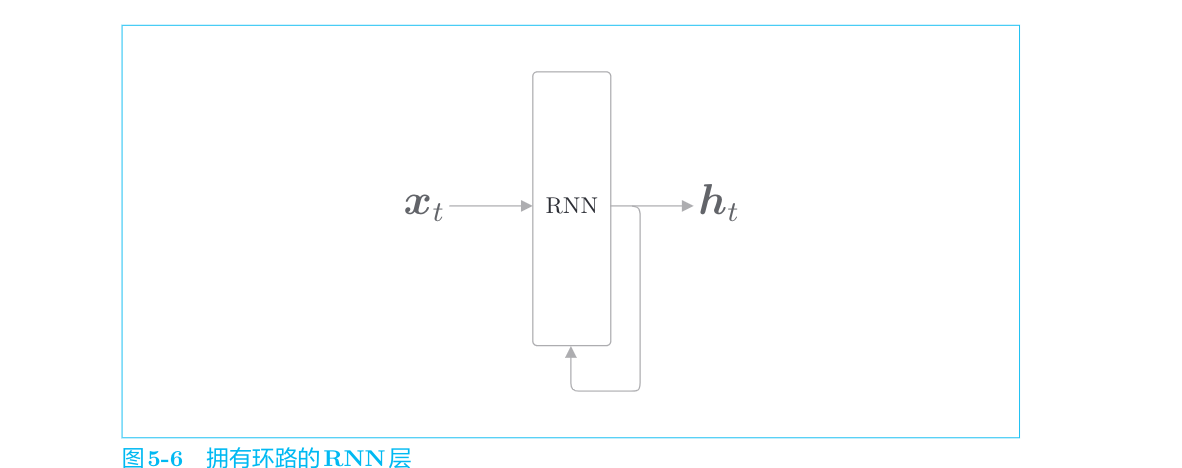
通过该环路,数据可以在层内循环。在图5-6中,时刻
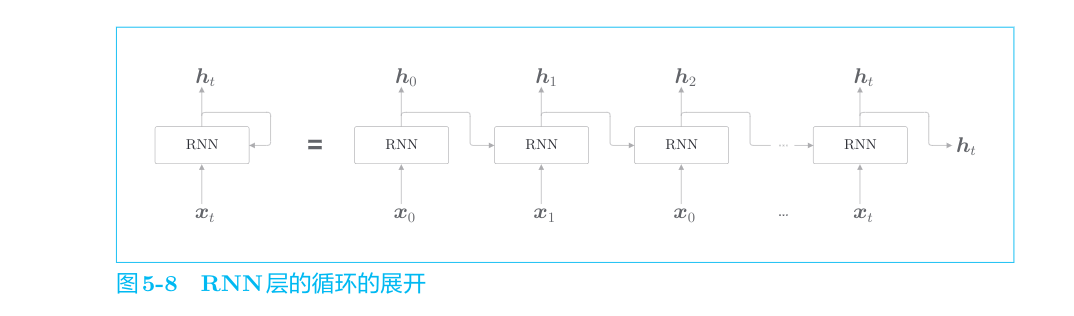
由图5-8可以看出,各个时刻的RNN层接收传给该层的输入和前一个RNN层的输出,然后据此计算当前时刻的输出,此时进行的计算可以用下式表示:
RNN有两个权重,分别是将输入
Backpropagation Through Time
将循环展开后的RNN可以使用(常规的)误差反向传播法。因为这里的误差反向传播法是“按时间顺序展开的神经网络的误差反向传播法”,所以称为Backpropagation Through Time(基于时间的反向传播),简称BPTT。

Truncated BPTT
在处理长时序数据时,通常的做法是将网络连接截成适当的长度。具体来说,就是将时间轴方向上过长的网络在合适的位置进行截断,从而创建多个小型网络,然后对截出来的小型网络执行误差反向传播法,这个方法称为Truncated BPTT(截断的BPTT)。
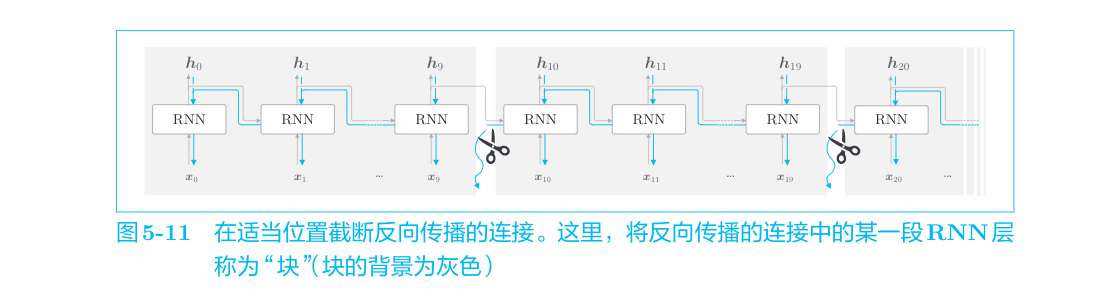
长短期记忆(Long short-term memory,LSTM)
RNN存在环路,可以记忆过去的信息,其结构非常简单,易于实现。不过,遗憾的是,这个RNN的效果并不好。原因在于,许多情况下它都无法很好地学习到时序数据的长期依赖关系。实际上,当我们说RNN时,更多的是指LSTM层,而不是上一章的RNN。顺便说一句,当需要明确指上一章的RNN时,我们会说“简单RNN”或“Elman”。
RNN的问题
梯度消失和梯度爆炸
RNN层通过向过去传递“有意义的梯度”,能够学习时间方向上的依赖关系。此时梯度(理论上)包含了那些应该学到的有意义的信息,通过将这些信息向过去传递,RNN层学习长期的依赖关系。但是,如果这个梯度在中途变弱(甚至没有包含任何信息),则权重参数将不会被更新。也就是说,RNN层无法学习长期的依赖关系。不幸的是,随着时间的回溯,这个简单RNN未能避免梯度变小(梯度消失)或者梯度变大(梯度爆炸)的命运。
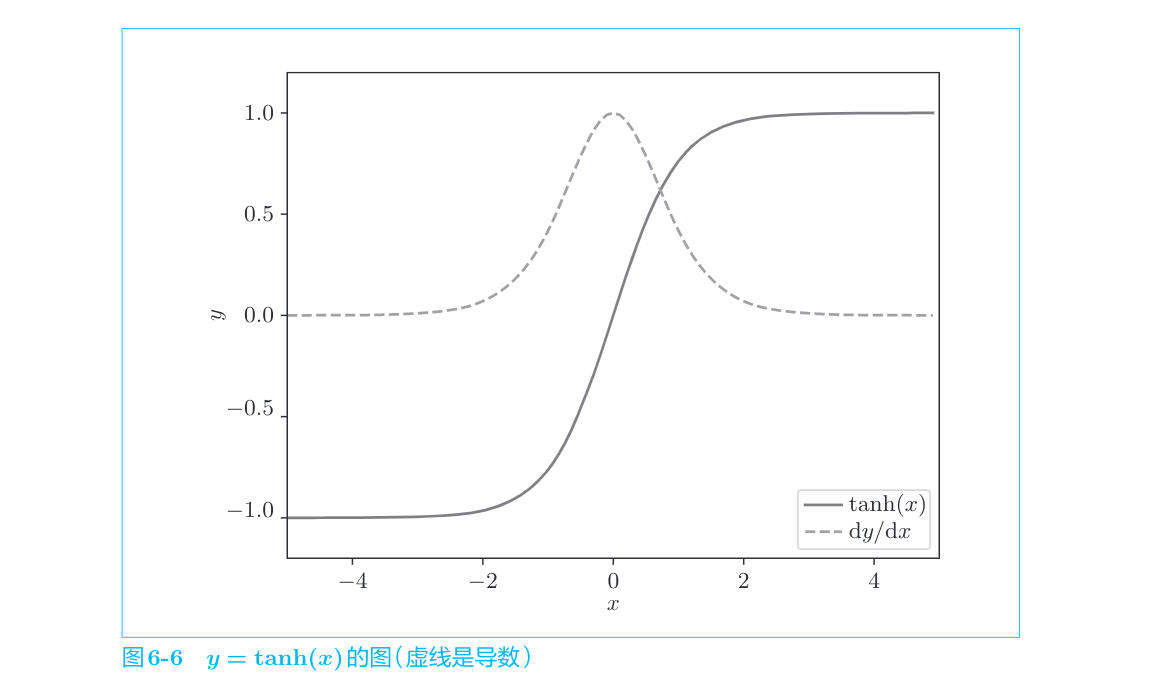
虚线是y=tanh(x)的导数。从图中可以看出,它的值小于1.0,并且随着x远离0,它的值在变小。这意味着,当反向传播的梯度经过tanh节点时,它的值会越来越小。因此,如果经过tanh函数T次,则梯度也会减小T次。
梯度爆炸对策
解决梯度爆炸有既定的方法,称为梯度裁剪(gradients clipping)。
假设可以将神经网络用到的所有参数的梯度整合成一个,并用符号ˆg表示。另外,将阈值设置为threshold。此时,如果梯度的L2范数‖ˆg‖大于或等于阈值,就按上述方法修正梯度,这就是梯度裁剪。如你所见,虽然这个方法很简单,但是在许多情况下效果都不错。
梯度消失和LSTM
LSTM层的结构
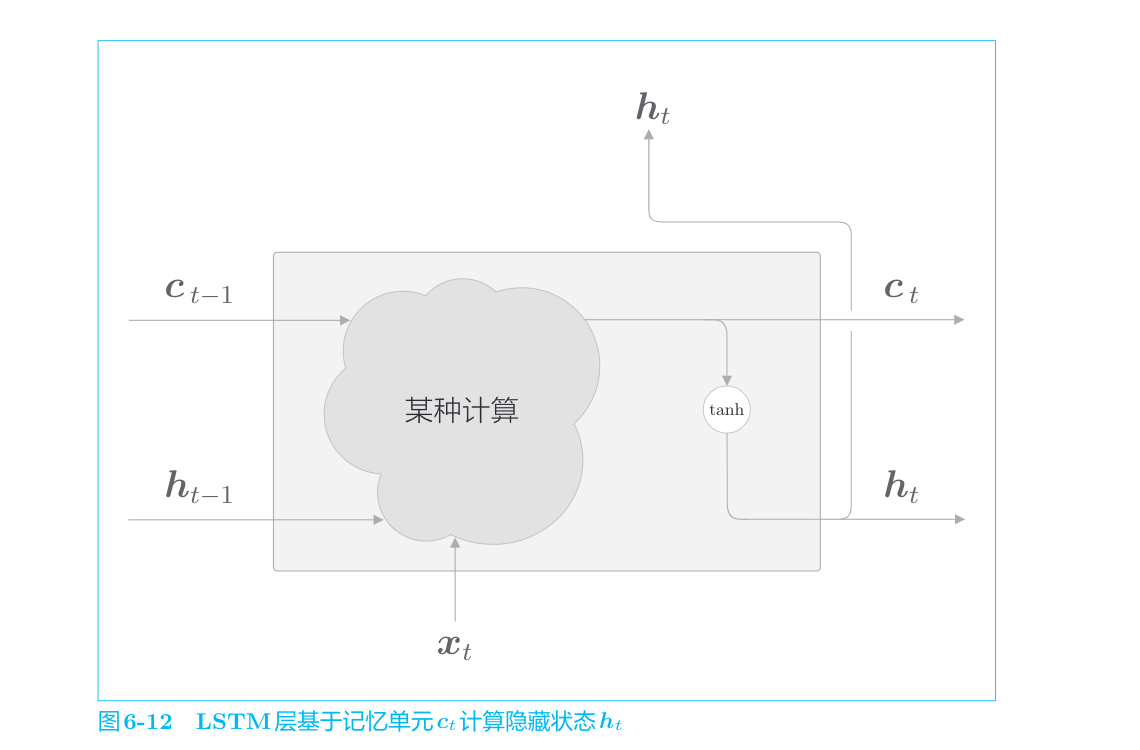
LSTM有记忆单元
当前的记忆单元
输出门
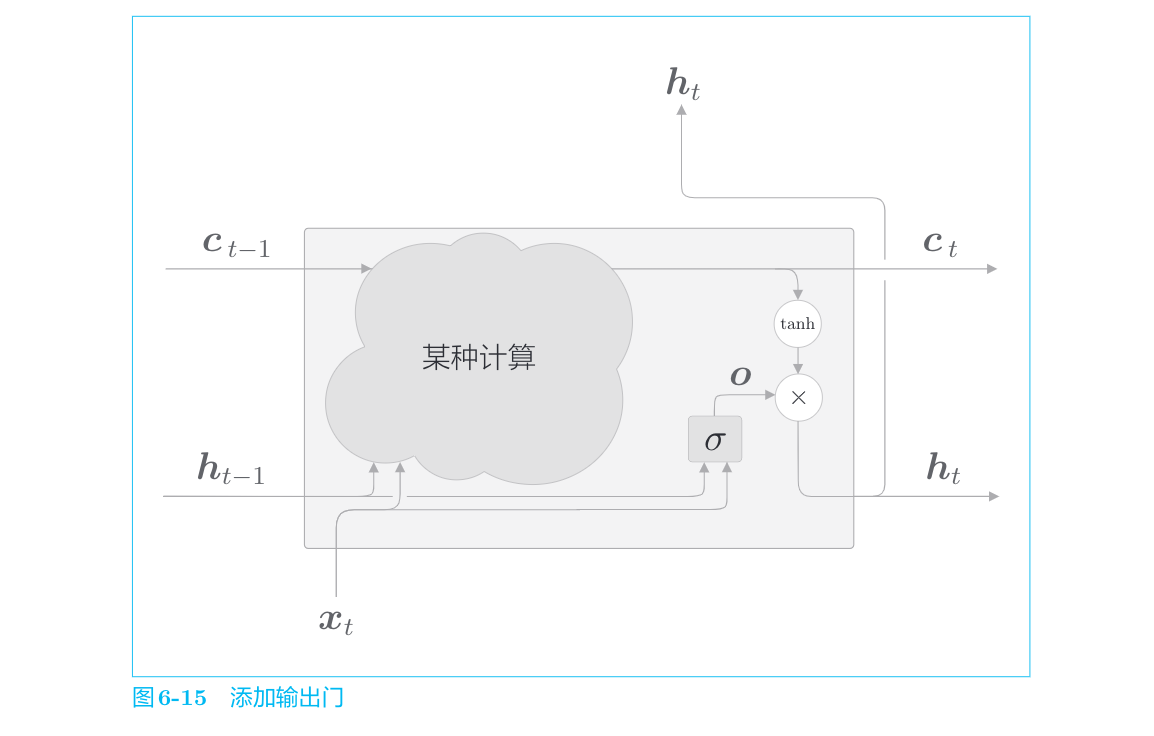
针对
输出门的开合程度(流出比例)根据输入xt和上一个状态ht−1求出。这里在使用的权重参数和偏置的上标上添加了output的首字母o。之后,我们也将使用上标表示门。另外,sigmoid函数用σ()表示。
输入
将输出门进行的式(6.1)的计算表示为
遗忘门
在记忆单元ct−1上添加一个忘记不必要记忆的门,这里称为遗忘门(forget gate)。
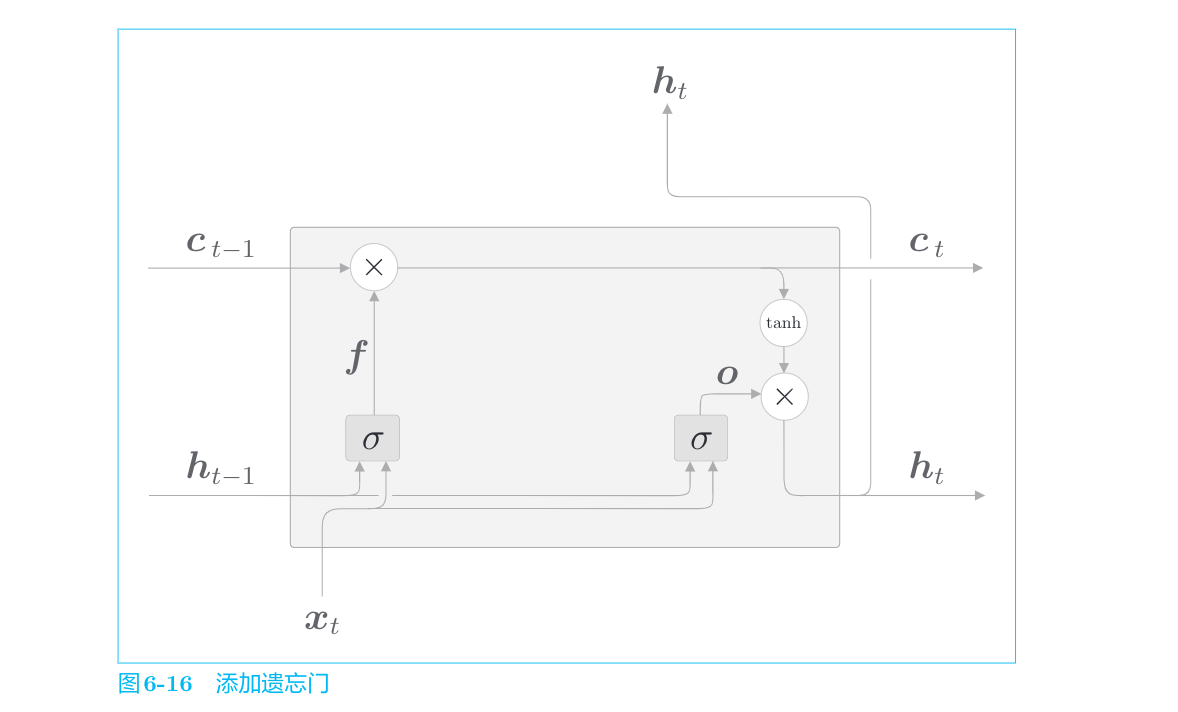
将遗忘门进行的一系列计算表示为σ,其中有遗忘门专用的权重参数,此时的计算如下:
新的记忆单元
遗忘门从上一时刻的记忆单元中删除了应该忘记的东西,但是这样一来,记忆单元只会忘记信息。现在我们还想向这个记忆单元添加一些应当记住的新信息,为此我们添加新的tanh节点。
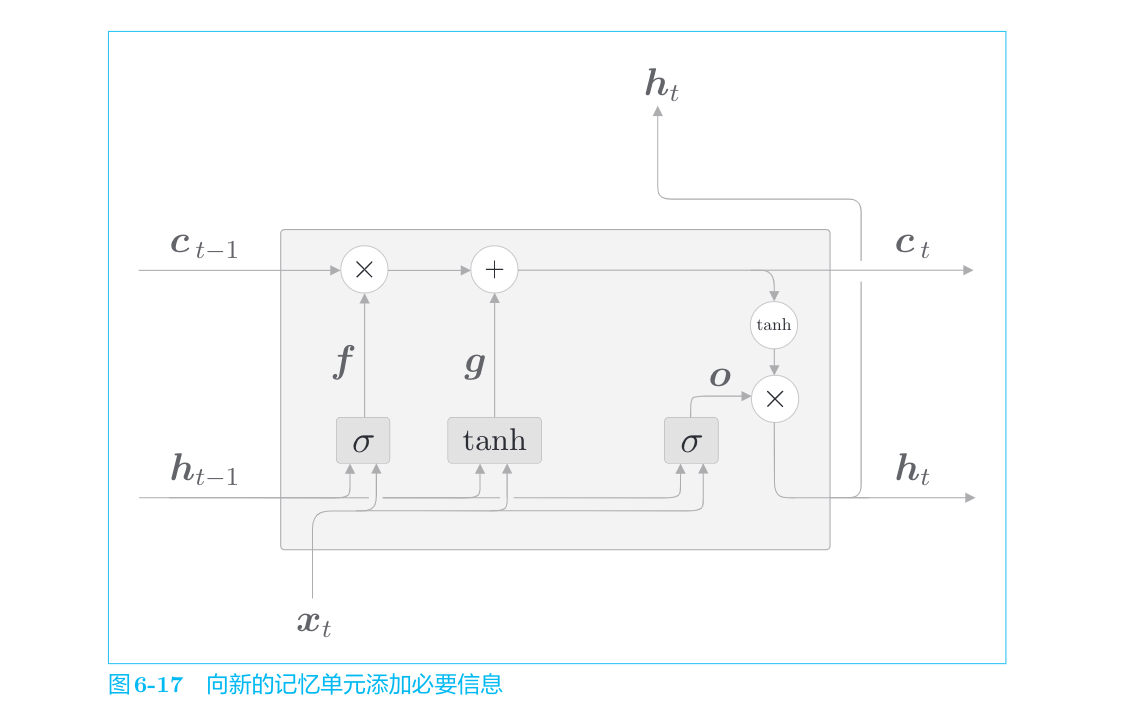
输入门
最后,我们给图6-17的
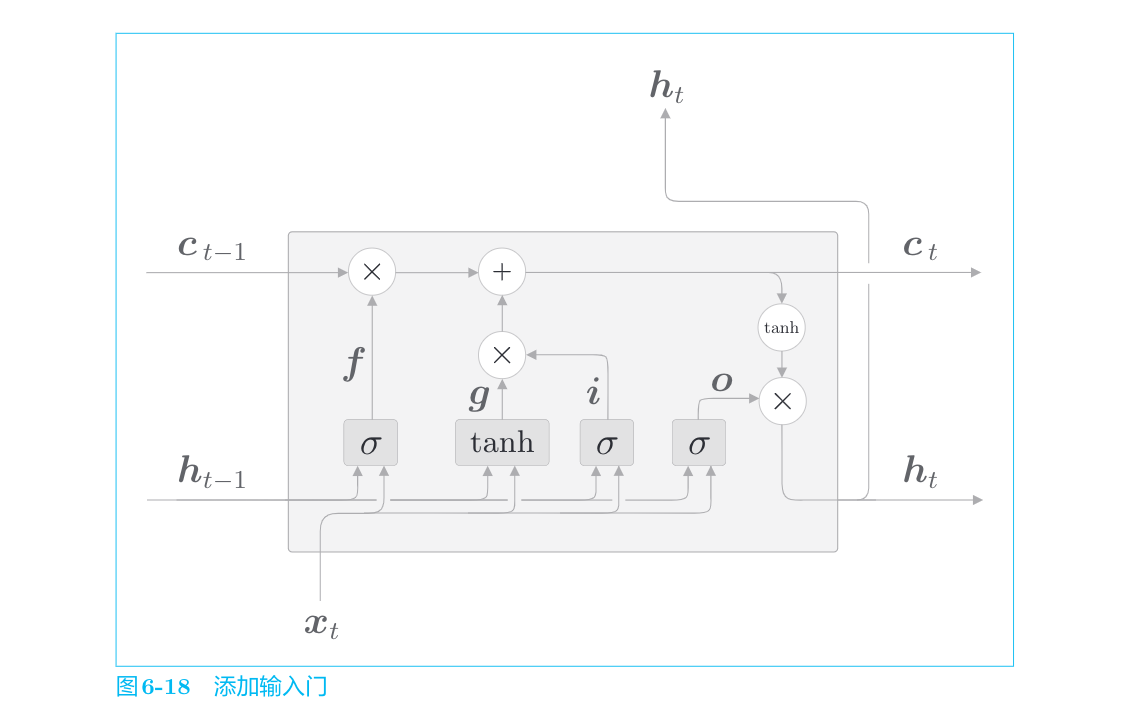
输入门判断新增信息g的各个元素的价值有多大。输入门不会不经考虑就添加新信息,而是会对要添加的信息进行取舍。输入门会添加加权后的新信息。
用σ表示输入门,用i表示输出,此时进行的计算如下所示:
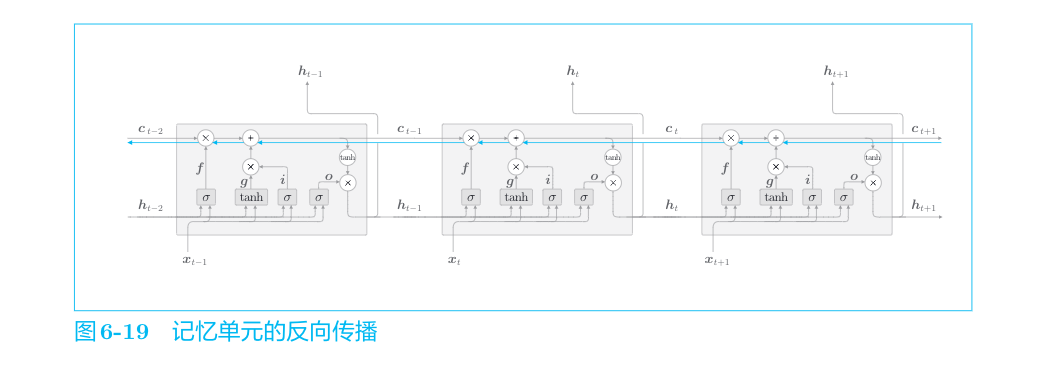
LSTM的梯度的流动
seq2seq
世界上存在许多输入输出均为时序数据的任务。从现在开始,我们会考察将时序数据转换为其他时序数据的模型。作为它的实现方法,我们将介绍使用两个RNN的seq2seq模型。
seq2seq的原理
seq2seq模型也称为Encoder-Decoder模型。顾名思义,这个模型有两个模块——Encoder(编码器)和Decoder(解码器)。编码器对输入数据进行编码,解码器对被编码的数据进行解码。
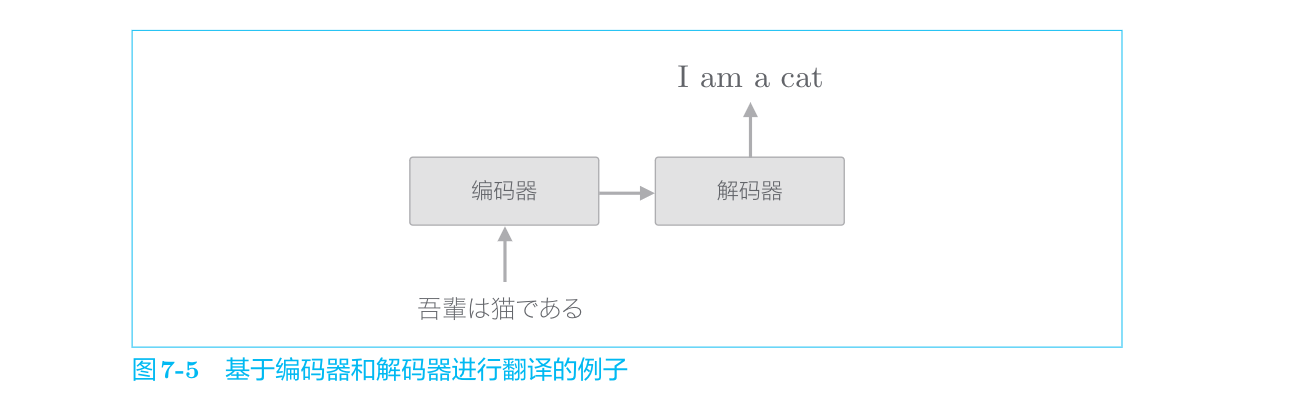
吾輩は猫である”这句话进行编码,然后将编码好的信息传递给解码器,由解码器生成目标文本。此时,编码器编码的信息浓缩了翻译所必需的信息,解码器基于这个浓缩的信息生成目标文本。
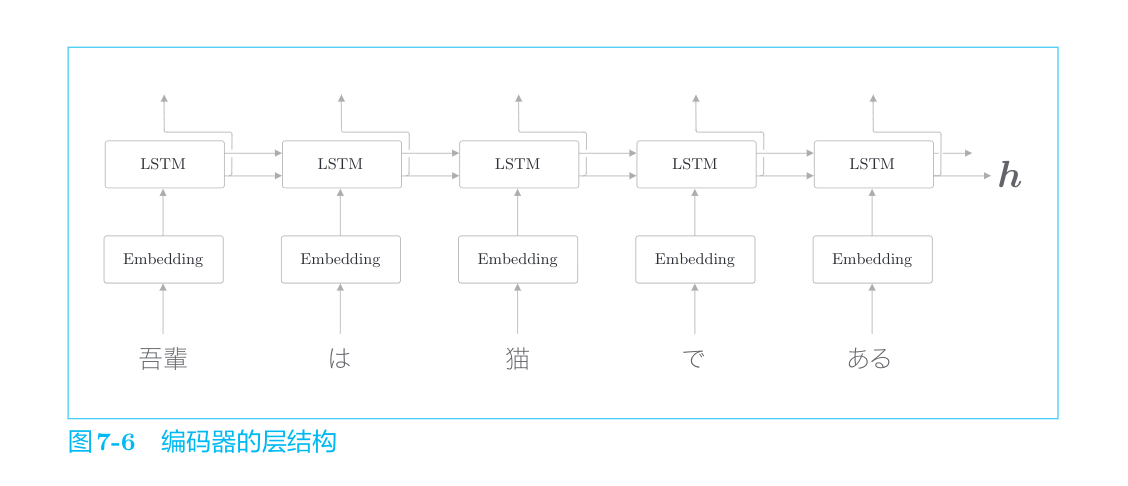
编码器利用RNN将时序数据转换为隐藏状态h。这里的RNN使用的是LSTM,不过也可以使用“简单RNN”或者GRU等。另外,这里考虑的是将日语句子分割为单词(而不是单个字符)进行输入的情况。
编码器输出的向量h是LSTM层的最后一个隐藏状态,其中编码了翻译输入文本所需的信息。这里的重点是,LSTM的隐藏状态h是一个固定长度的向量。说到底,编码就是将任意长度的文本转换为一个固定长度的向量(分布式表示)。
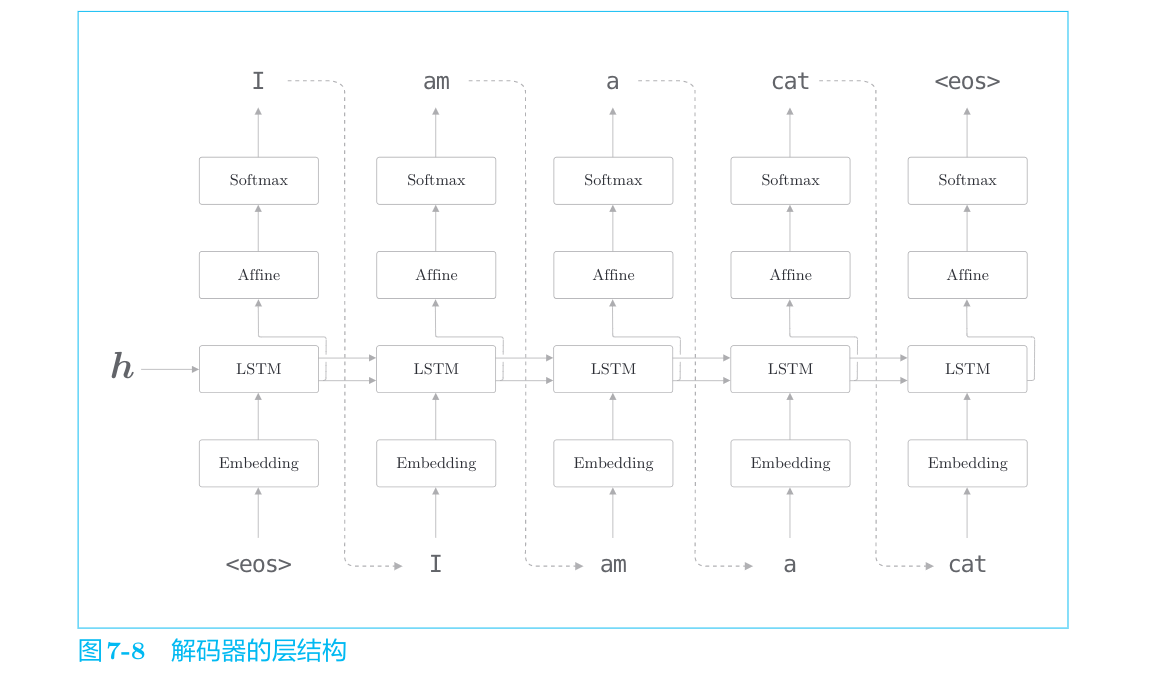
解码器的结构和上一节的神经网络完全相同。不过它和上一节的模型存在一点差异,就是LSTM层会接收向量h。在上一节的语言模型中,LSTM层不接收任何信息(硬要说的话,也可以说LSTM的隐藏状态接收“0向量”)。这个唯一的、微小的改变使得普通的语言模型进化为可以驾驭翻译的解码器。
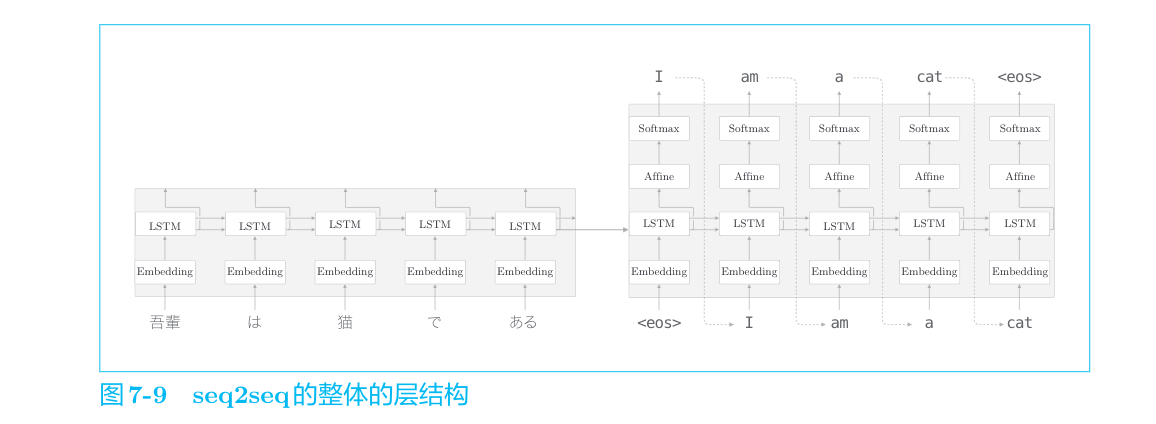
seq2seq由两个LSTM层构成,即编码器的LSTM和解码器的LSTM。此时,LSTM层的隐藏状态是编码器和解码器的“桥梁”。在正向传播时,编码器的编码信息通过LSTM层的隐藏状态传递给解码器;在反向传播时,解码器的梯度通过这个“桥梁”传递给编码器。
注意力机制(Attention Mechanism,Attention)
Attention的结构
seq2seq存在的问题
eq2seq中使用编码器对时序数据进行编码,然后将编码信息传递给解码器。此时,编码器的输出是固定长度的向量。实际上,这个“固定长度”存在很大问题。因为固定长度的向量意味着,无论输入语句的长度如何(无论多长),都会被转换为长度相同的向量。实际上在很多问题中输入输出长度并不一定是一对一的关系。
编码器的改进
使用各个时刻(各个单词)的隐藏状态向量,可以获得和输入的单词数相同数量的向量。在图8-2的例子中,输入了5个单词,此时编码器输出5个向量。这样一来,编码器就摆脱了“一个固定长度的向量”的制约。
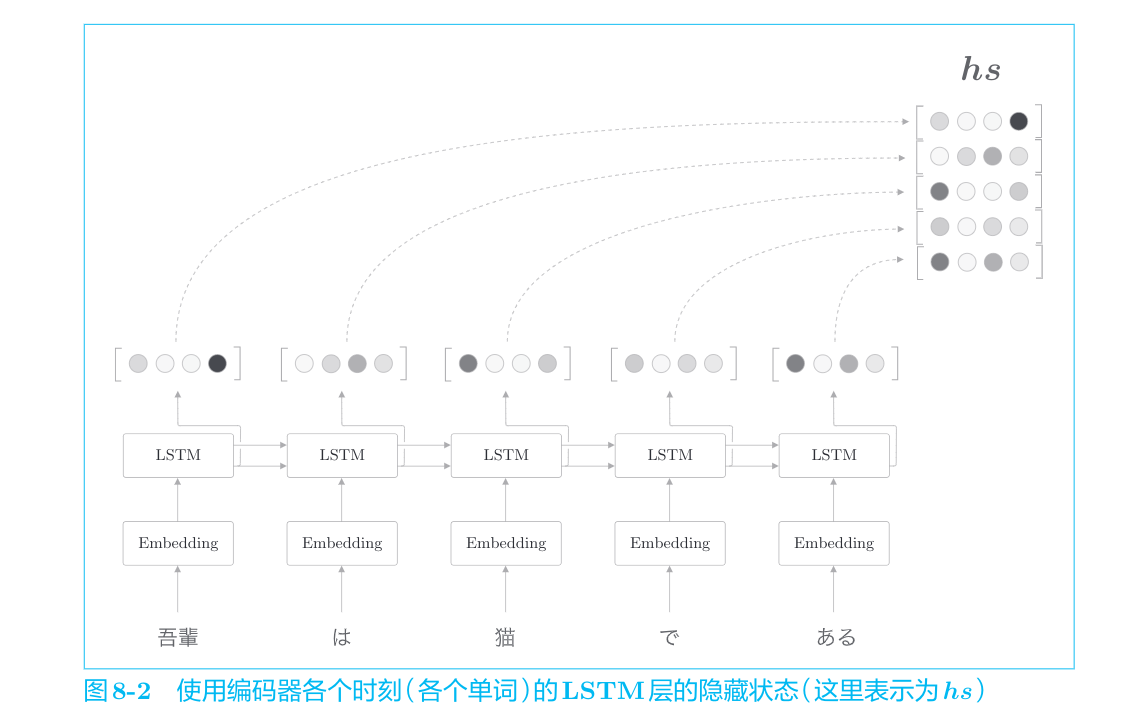
这一步在Keras中,在初始化RNN层时,可以设置return_sequences为True或者False。
各个时刻的LSTM层的隐藏状态中包含了大量当前时刻的输入单词的信息,编码器输出的hs矩阵就可以视为各个单词对应的向量集合。
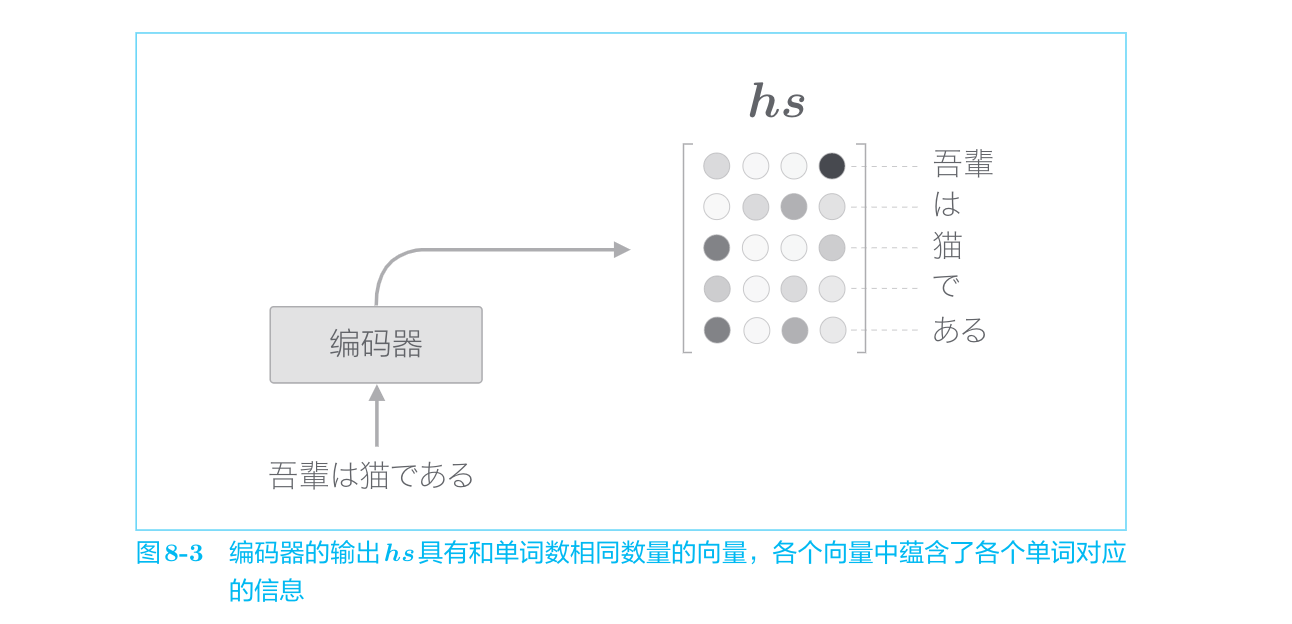
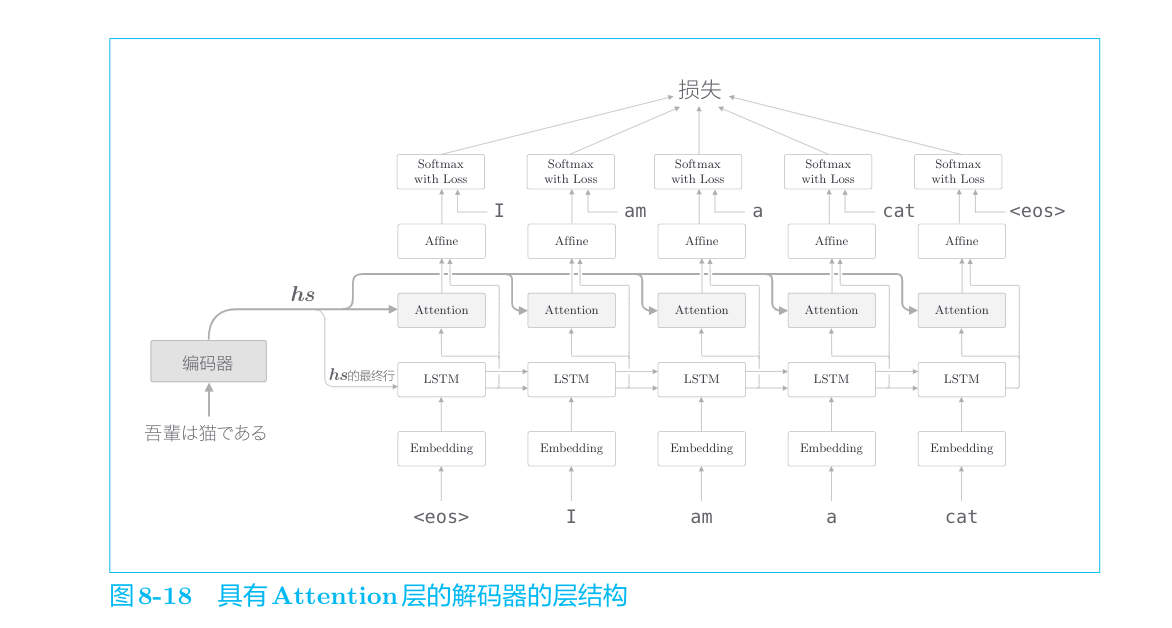
解码器的改进
编码器整体输出各个单词对应的LSTM层的隐藏状态向量hs。然后,这个hs被传递给解码器,以进行时间序列的转换。
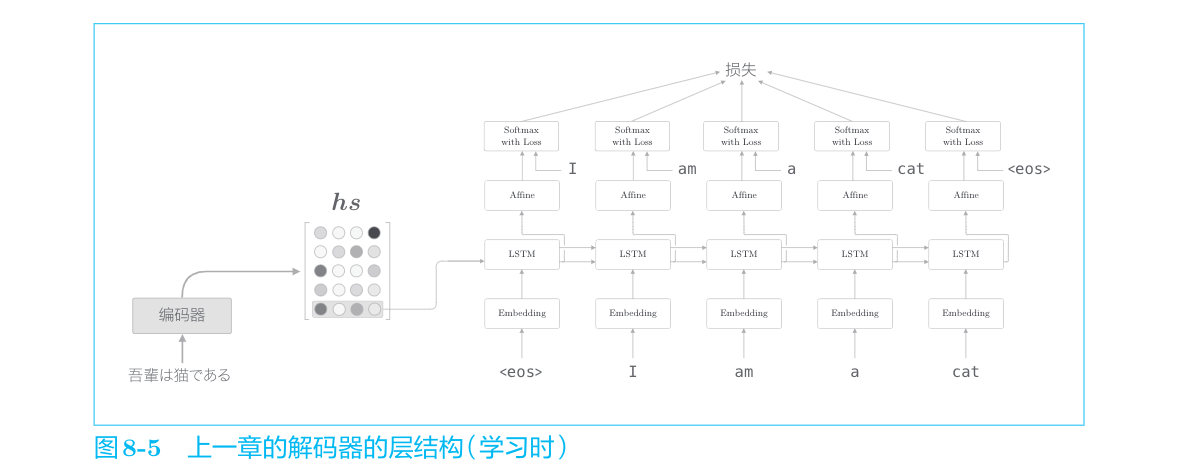
上一章的解码器只用了编码器的LSTM层的最后的隐藏状态。如果使用hs,则只提取最后一行,再将其传递给解码器。下面我们改进解码器,以便能够使用全部
从现在开始,我们的目标是找出与“翻译目标词”有对应关系的“翻译源词”的信息,然后利用这个信息进行翻译。也就是说,我们的目标是仅关注必要的信息,并根据该信息进行时序转换。这个机制称为Attention,是本章的主题。
我们新增一个进行“某种计算”的层。这个“某种计算”接收(解码器)各个时刻的LSTM层的隐藏状态和编码器的
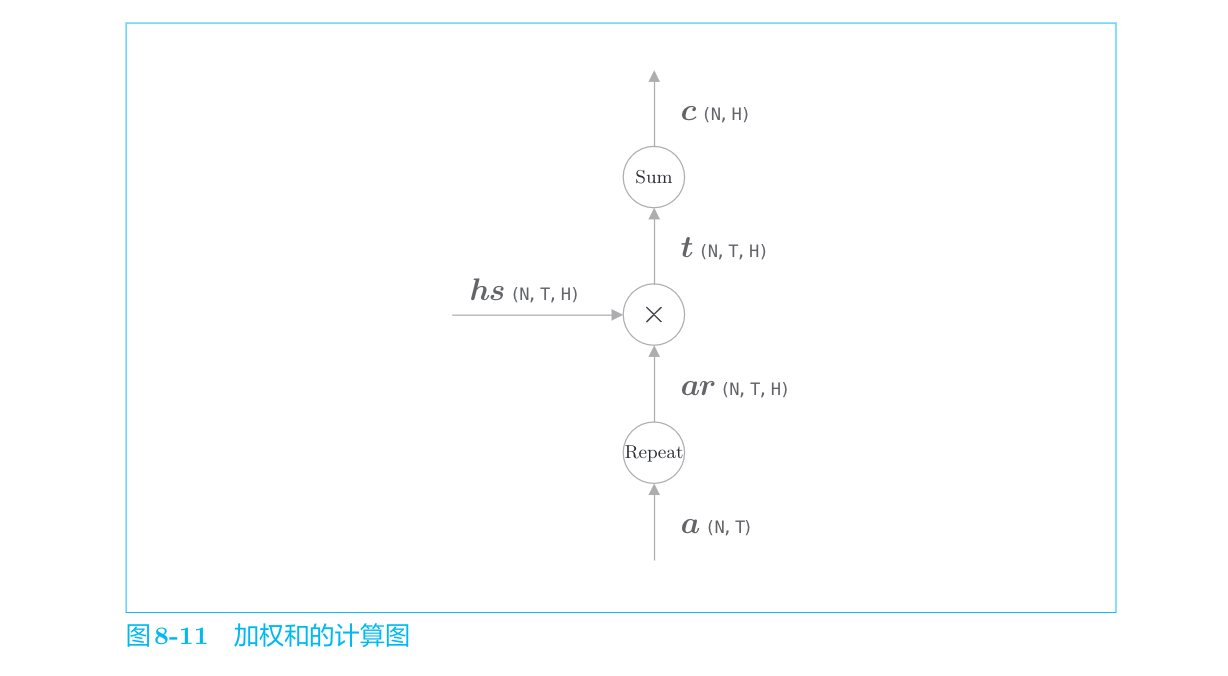
Weight Sum层
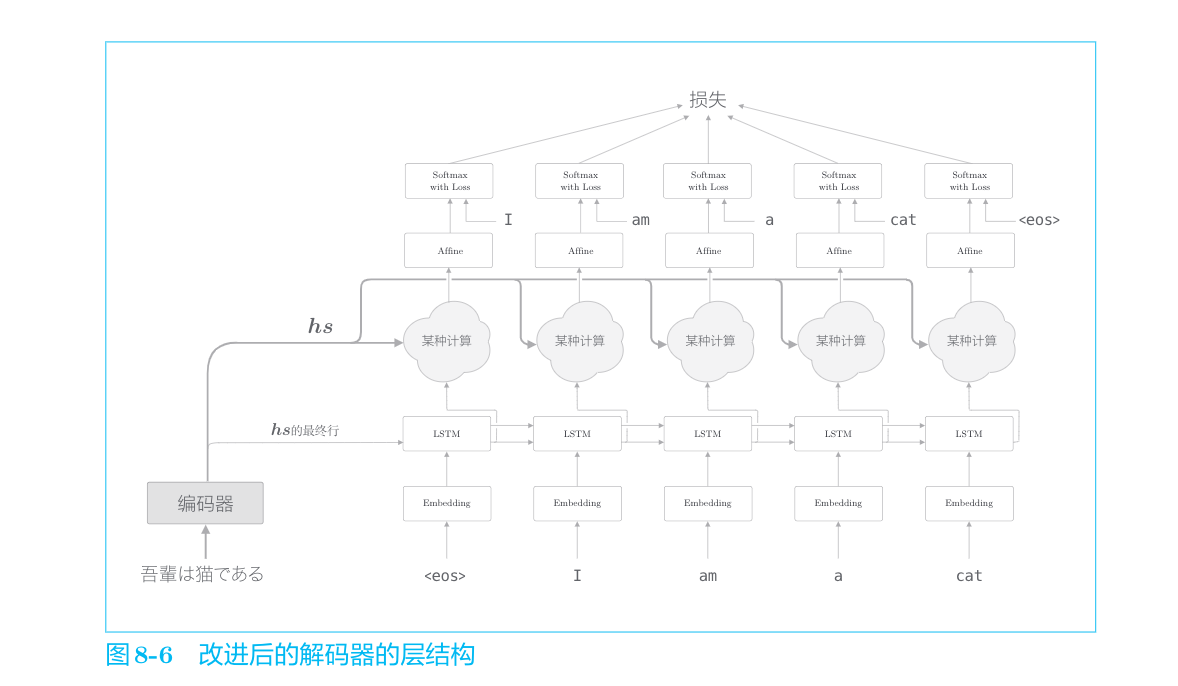
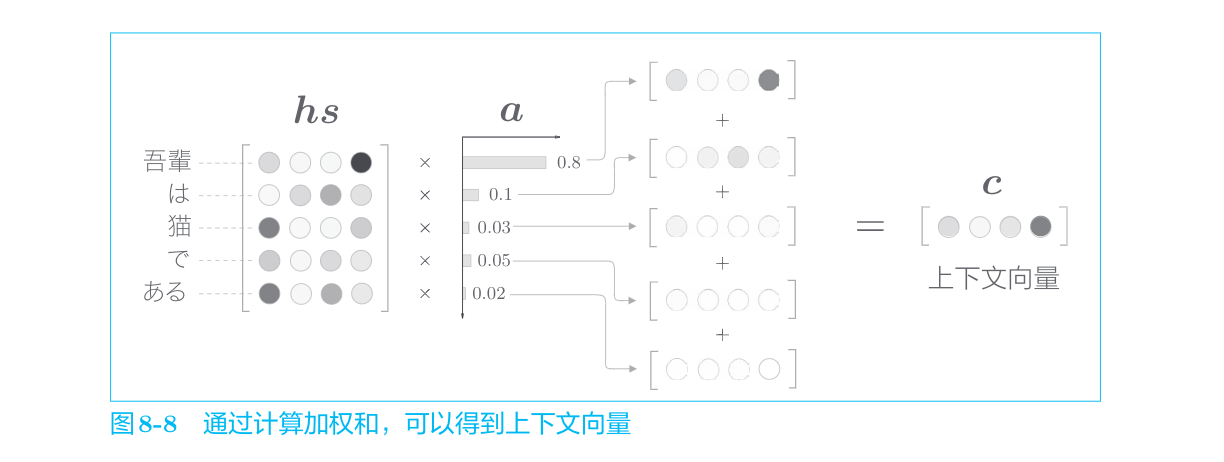
网络所做的工作是提取单词对齐信息。具体来说,就是从
这里使用了表示各个单词重要度的权重(记为
Attention Weight层
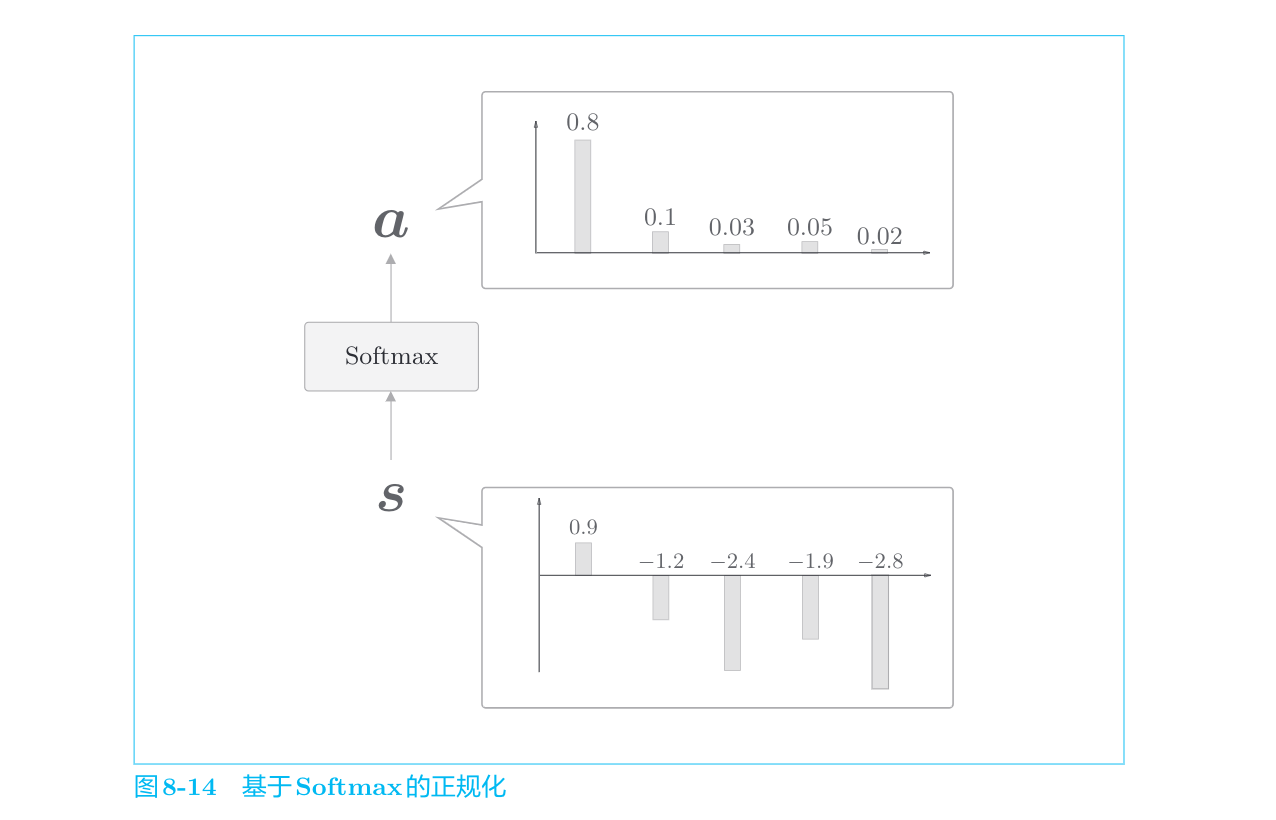
表示各个单词重要度的权重
这里通过向量内积算出
计算向量相似度的方法有好几种。除了内积之外,还有使用小型的神经网络输出得分的做法。文献[49]中提出了几种输出得分的方法。

综合分析
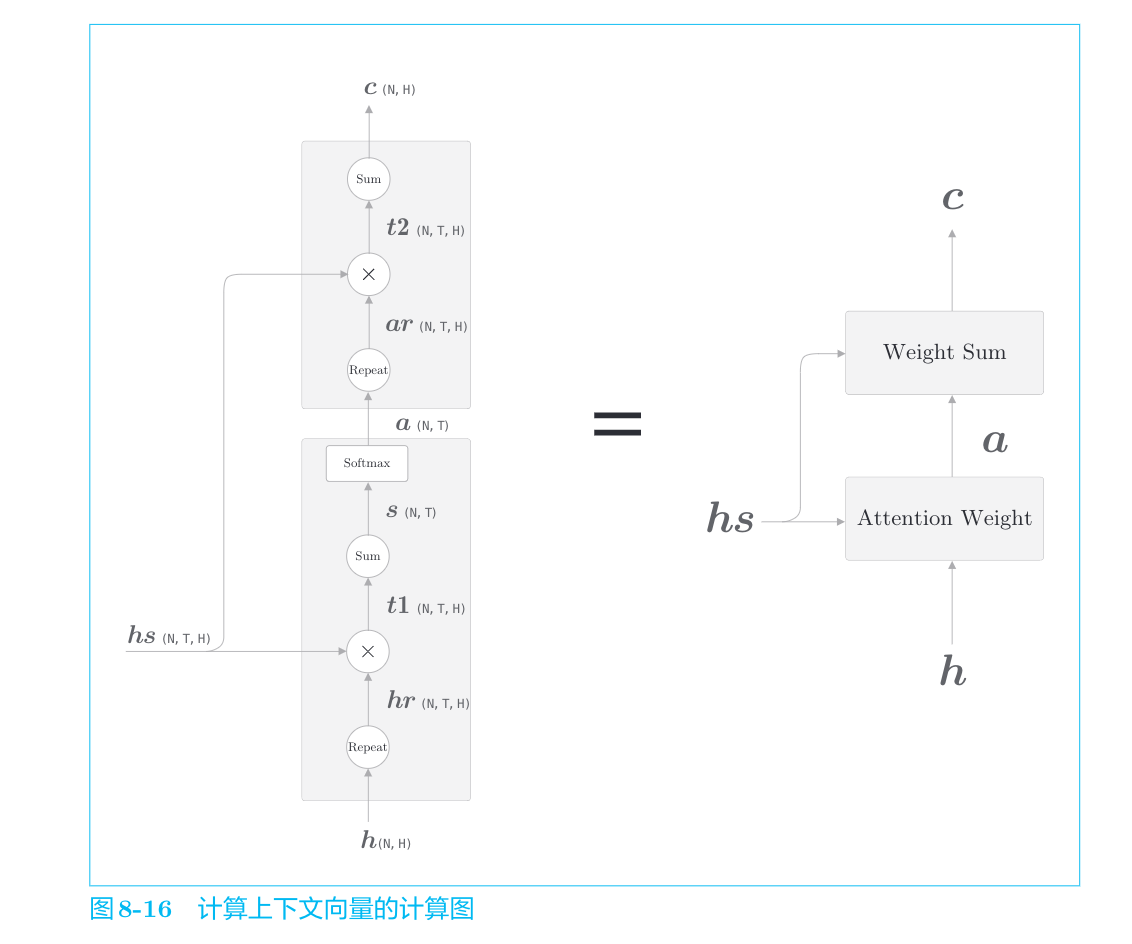
我们已经分为Weight Sum层和Attention Weight层进行了实现。重申一下,这里进行的计算是:Attention Weight层关注编码器输出的各个单词向量

Comments | NOTHING