摘要

特征工程一直是许多预测模型成功的关键。然而，这个过程并不简单，通常需要手动的特征工程或详尽的搜索。DNN能够自动学习特征的相互作用；然而，它们隐含地产生了所有的相互作用，并且在学习所有类型的交叉特征方面不一定有效。在本文中，我们提出了Deep & Cross Network（DCN），它保持了DNN模型的优点，除此之外，它还引入了一种新型的交叉网络，在学习某些有限阶数的特征交互方面更有效率。特别是，DCN在每一层都明确地应用了特征交叉，不需要手动的特征工程，并且增加的额外复杂性是可以忽略的。我们的实验结果表明，在CTR预测数据集和密集分类数据集上，它在模型准确性和内存使用方面都优于最先进的算法。

引言

点击率（CTR）的预测是一个大规模的问题，对数十亿美元的在线广告行业至关重要。在广告业中，广告商向出版商付费，在出版商的网站上展示他们的广告。一种流行的支付模式是每次点击成本（CPC）模式，广告商只有在发生点击时才被收取费用。因此，出版商的收入在很大程度上依赖于准确预测点击率的能力。

识别频繁的且可预测的特征并同时探索看不见或罕见的交叉特征是做出良好预测的关键。然而，web应用规模的推荐系统的数据大多是离散的和类别特征，导致了一个大而稀疏的特征空间，对特征探索来说是一个挑战。这使得大多数大规模的系统仅限于线性模型，如逻辑回归。

线性模型[3]简单、可解释且易于扩展；然而，它们的表达能力有限。另一方面，交叉特征已被证明对提高模型的表现力具有重要意义。不幸的是，这需要手动的特征工程或详尽的搜索来识别这些特征；此外，对未见过的特征互动进行归纳也很困难。

在本文中，我们旨在通过引入一种新的神经网络结构--交叉网络--来避免特定任务的特征工程，该网络以一种自动的方式明确应用特征交叉。每一层都在现有的基础上产生高阶的相互作用，并保留前几层的相互作用。我们将交叉网络与深度神经网络（DNN）[10, 14]联合训练。DNN有希望捕捉到非常复杂的特征间的相互作用；然而，与我们的交叉网络相比，它需要更多的参数，不能明确地形成交叉特征，并且可能无法有效地学习某些类型的特征间的相互作用。然而，联合训练交叉和DNN组件，可以有效地捕捉预测性的特征互动，并在CriteoCTR数据集上提供最先进的性能。

相关工作

由于数据集的大小和维度的急剧增加，人们提出了许多方法来避免广泛的特定任务的特征工程，主要是基于嵌入技术和神经网络。

因式分解机（FMs）[11, 12]将稀疏的特征投射到低维密集的向量上，并从向量内积中学习特征的相互作用。领域感知因式分解机（FFMs）[7, 8]进一步允许每个特征学习几个向量，每个向量与一个领域相关。遗憾的是，FMs和FFMs的浅层结构限制了它们的表达能力。已经有工作将FMs扩展到高阶[1, 18]，但一个缺点是它们有大量的参数，产生了不理想的计算成本。由于嵌入向量和非线性激活函数，深度神经网络（DNN）能够学习非琐碎的高阶特征相互作用。残差网络[5]最近的成功使得非常深的网络的训练成为可能。深度交叉[15]扩展了残差网络，并通过堆叠所有类型的输入实现了自动特征学习。

深度学习的显著成功引起了对其表达能力的理论分析。有研究[16, 17]表明，在给定足够多的隐藏单元或隐藏层的情况下，DNNs能够在一定的平滑度假设下以任意的精度近似一个任意的函数。一个关键原因是，大多数实际感兴趣的函数都不是任意的。

然而，剩下的一个问题是，DNN是否真的是代表这种实际利益的功能的最有效的方法。在Kaggle竞赛中，许多获奖方案中的人工筛选的特征是低阶的、明确的格式且有效的。另一方面，DNN学习的特征是隐性的和高度非线性的。这为设计一个能够比通用 DNN 更有效、更明确地学习有界度特征交互的模型提供了启示。

Wide & Deep[4]是一个符合这种想法的模型。它将交叉特征作为线性模型的输入，并与DNN模型共同训练线性模型。然而，Wide & Deep的成功取决于对交叉特征的适当选择，这是一个指数级的问题，目前还没有明确的有效方法。

主要贡献

在本文中，我们提出了Deep & Cross Network（DCN）模型，该模型能够在稀疏和密集输入的情况下实现大规模互联网应用的自动特征学习。DCN有效地捕捉了有效的有限阶数的特征互动，学习高度非线性的互动，不需要手动的特征工程或详尽的搜索，并具有低计算成本。

本文的主要贡献包括：

• 我们提出了一种新型的交叉网络，它在每一层都明确地应用了特征交叉，有效地学习了有限阶数的预见性交叉特征，并且不需要人工特征工程或详尽的搜索。
• 交叉网络是简单而有效的。根据设计，最高多项式的次数在每一层都会增加，并由层深决定。网络由所有最高次数的交叉项组成，它们的系数都不同。
• 交叉网络的内存效率高，而且容易实现。
• 我们的实验结果表明，在交叉网络的情况下，DCN的对数损失比DNN低，而参数数量几乎少了一个数量级。

本文组织如下。第2节描述了DCN网络的架构。第3节详细分析了交叉网络。第4节展示了实验结果。

DEEP & CROSS NETWORK (DCN)

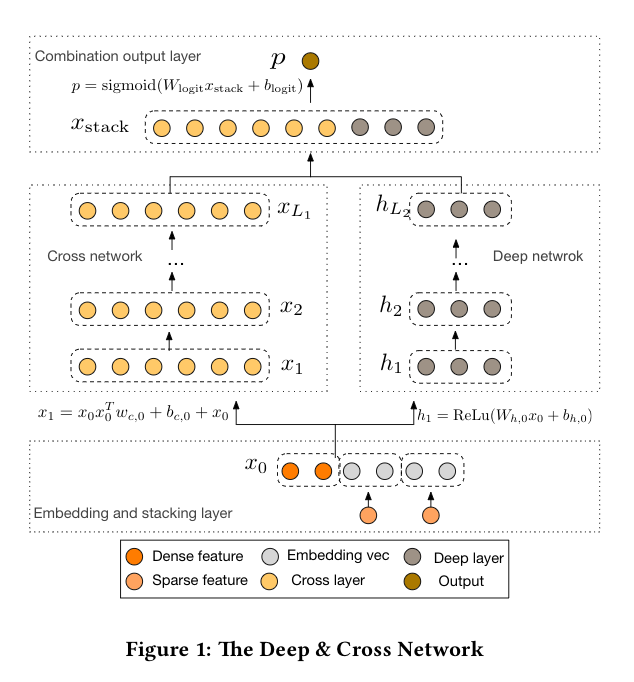
在这一节中，我们描述了深度和交叉网络工作（DCN）模型的架构。一个DCN模型从一个嵌入和堆叠层开始，然后是交叉网络和一个并行的深度网络。然后是最后的组合层，将两个网络的输出结合起来。完整的DCN模型见图1。

嵌入和堆叠层

我们考虑具有稀疏和密集特征的输入数据。在大规模互联网应用的推荐系统中，如CTR预测，输入数据大多是分类特征，如 "country=usa"。这类特征通常被编码为onehot向量，例如"[0,1,0]"；然而，对于大型字典来说，这可能会导致过高的维度特征空间。

为了降低维度，我们采用嵌入处理将这些二进制特征转化为密集的实值向量（通常称为嵌入向量）：

$X_{embed,i}$代表嵌入向量，$X_{i}$是第$i$个特征的二进制形式输入，$X_{embed,i}\in \mathbb{R}^{n_e \times n_v}$是相应的嵌入矩阵，将与网络中的其他参数一起被优化，$n_e$与$n_v$分别是嵌入输出大小与词汇表大小。

最后，我们将嵌入向量与归一化的密集特征$x_{dense}$一起堆叠成一个向量：

并将$X_0$送入神经网络。

交叉网络

我们的新型交叉网络的关键思想是以一种有效的方式应用明确的特征交叉。交叉网络由交叉层组成，每一层都有以下公式：

$X_l,{X}_{l+1} \in \mathbb{R}^d$是用于表示第$l$层与$(l+1)$层交叉层输出的列向量；$W_l,b_l \in \mathbb{R}^d$代表第$l$层的权重与偏差。每个交叉层在特征交叉函数$f$后，将其输入加回，而映射函数$f$：$\mathbb{R}^d \mapsto \mathbb{R}^d$拟合了$X_{l+1} - X_l$的残差。图2显示了一个交叉层的可视化情况。

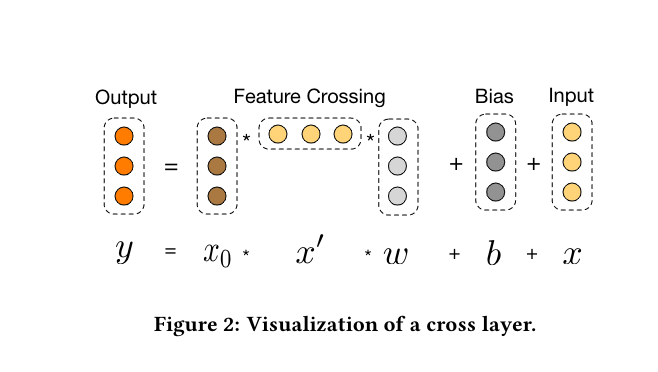
交叉网络的特殊结构使交叉特征的阶数随着层的深度而增长。一个$l$层的交叉网络的最高多项式次数（以输入$x_0$计）是$l+1$。事实上，交叉网络包括所有次数为1到$l+1$的交叉项$x^{α_1}_1x^{α_2}_2\cdots x^{α_d}_d$ 。详细分析见第3节。

复杂度分析。让$L_c$表示交叉层的数量，$d$表示输入维度。那么，交叉网络中涉及的参数数量为

交叉网络的时间和空间复杂性在输入维度上是线性的。因此，与深度神经网络相比，交叉网络引入的复杂度可以忽略不计，使DCN的整体复杂度与传统DNN的复杂度保持一致。这种效率得益于$X_0X^T_l$矩阵的秩为一属性，它使我们能够在不计算或存储整个矩阵的情况下生成所有交叉项。

交叉网络的少量参数限制了模型的容量。为了捕捉高度非线性的相互作用，我们引入了一个并行的深度网络。

深度网络

深度网络是一个全连接的前馈神经网络工作，每个层具有以下形式：

$h_l \in \mathbb{R}^n_{l}$，$h_{l+1} \in \mathbb{R}^n_{l+1}$分别代表第$l$与第$l+1$个隐藏层；$W_l \in \mathbb{R}^{n_{l+1} \times n_l}$，$b_l \in \mathbb{R}^{n_{l+1} }$是第$l$层的权重与偏差；$f(\cdot)$是ReLU函数。

复杂性分析。为简单起见，我们假设所有的深度神经网络层都是同等大小的。让$L_d$表示深度神经网络层的数量，$m$表示深度神经网络层的大小。那么，深度神经网络层网络中的参数数量为：

联合层

组合层将两个网络的输出连接起来，并将连接的向量送入标准的对数层。

以下是一个两类分类概率的公式：

$X_{L_1} \in \mathbb{R}^d$ ，$h_{L_2} \in \mathbb{R}^d$分别代表交叉网络与深度神经网络的输出，$W_{logits} \in \mathbb{R}^{d+m}$是联合层的权重向量 ，$\sigma (x)=1/(1+exp(-x))$。

损失函数是带有一个正则化项的对数损失，

$p_i$是由公式5计算出的概率，$y_i$是实际正确的label，$N$是输入的总数，$\lambda$是L2正则化参数。

我们联合训练这两个网络，因为这允许每个单独的网络在训练过程中了解其他网络的情况。

交叉网络分析

在本节中，我们分析了DCN的交叉网络，以了解其有效性。我们提供了三个角度：多项式近似，对FM的概括，以及有效的投影。为了简单起见，我们假设$b_i=0$。

为了方便表示。将$W_j$中的第$i$个元素表示成$W^{(i)}_j$。对于$\boldsymbol{\alpha} = [\alpha_1,\cdots,\alpha_d] \in \mathbb{N}^d$与$X=[x_1,\cdots,x_d] \in \mathbb{R}^d$，我们定义$|\boldsymbol{\alpha}|=\sum^d_{i=1}\alpha_i$。

$|\boldsymbol{\alpha}|$定义了交叉项的阶数$x_1^{\alpha_1} x_2^{\alpha_2} \cdots x_d^{\alpha_d}$，多项式的次数是由其项的最高次数决定的。

多项式近似

根据Weierstrass近似定理[13]，在一定的平稳性假设下，任何函数都可以被多项式近似到一个任意的精度。因此，我们从多项式近似的角度来分析交叉网络的工作。特别是，交叉网络以一种高效的、可表达的、可推广到现实世界数据集的方式来近似相同程度的多项式类。

我们详细研究了交叉网络与同度多项式类的近似问题。让我们用$P_n(x)$表示$n$次的多变量多项式类。

这一类中的每个多项式都有$O(d_n)$个系数。我们表明，只要有$O(d)$个参数，交叉网络就包含了在相同程度的多项式中出现的所有交叉项，每个项的系数都是不同的。

定理3.1.考虑一个$l$层交叉网络，第$i+1$层定义为$X_{i+1}=X_0X_i^TW_i+X_i$。让网络的输入为$X_0=[x_1,x_2,\cdots,x_d]^T$，输出为$g_l(X_0)=x^T_lW_l$，参数为$W_i,b_i∈\mathbb{R}^d$。那么，多变量多项式$g_l(X_0)$再现以下类别的多项式：

$C_{\alpha}=M_{\alpha}\sum_{i\in B_\alpha}\sum_{j\in P_\alpha}\prod^{|\alpha|}_{k=1}W^{(j_k)}_{i_k}$其中$M_\alpha$常数独立于$W_i$，$i=[i_1,\cdots,i_{|\alpha|}]$与$j=[j_1,\cdots,j_{|\alpha|}]$是多指标，$B_{\alpha}=\{y\in \{{0,1,\cdots,l}\} |y_i <y_j\wedge y_{|\alpha|}=l \}^{|\alpha|}$，且$P_\alpha$是$(\underbrace{1,\cdots,1}_{\alpha_1 times}\cdots \underbrace{d,\cdots,d}_{\alpha_d times})$的所有排列组合的集合。

定理3.1的证明在附录中。让我们举个例子。当$\alpha=(1,1,1,0,\cdots,0)$达到某个常数时考虑$x_1 x_2 x_3$的系数$C_\alpha$，当$l=2$时$C_\alpha=\sum_{i,j,k \in P_\alpha}w^{(i)}_0w^{(j)}_1w^{(k)}_2$。当$l=2$时$C_\alpha=\sum_{i,j,k \in P_\alpha}w^{(i)}_0w^{(j)}_1w^{(k)}_3+w^{(i)}_0w^{(j)}_2w^{(k)}_3+w^{(i)}_1w^{(j)}_2w^{(k)}_3$。

FMs 的一般化

交叉网络与FM模型一样具有参数共享的思想，并进一步将其扩展到更深的结构中。

在FM模型中，特征$x_i$与一个权重向量$v_i$相关联，交叉项$x_ix_j$的权重由$〈v_i,v_j〉$计算得出。在DCN中，$x_i$与标量$\{w^{(i)}_k\}^l_{k=1}$相关，而$x_ix_j$的权重是来自$\{w^{(i)}_k\}^l_{k=0}$和$\{w^{(j)}_k\}^l_{k=0}$集合的参数的乘法。这两个模型的每个特征都学习了一些独立于其他特征的参数，而交叉项的权重是相应参数的某个组合。

参数共享不仅使模型更有效，而且还能使模型对未见过的特征交互进行泛化，并对噪声更加稳健。例如，以具有稀疏特征的数据集为例。如果两个二元特征$x_i$和$x_j$在训练数据中很少或从未出现，即$x_i\neq0∧x_j\neq0$，那么学到的$x_ix_j$的权重对预测没有意义。

FM是一个浅层结构，仅限于表示二阶的交叉项。相反，DCN能够构建所有的交叉项$x^{α_1}_1x^{α_2}_2...x^{α_d}_d$，其次数$|α|$由一些由层深度决定的常数所约束，如定理3.1所示。因此，交叉网络将参数共享的思想从单层延伸到多层和高阶交叉项。请注意，与高阶FM不同的是，交叉网络中的参数器数量只随输入深度的增加而线性增长。

高效投影

每个交叉层以有效率的方式将$X_0$和$X_l$之间的所有成对特征交互投射到输入的维度上。

考虑将$\tilde{x}∈\mathbb{R}^d$作为交叉层的输入。交叉层首先隐含地构建了$d^2$个成对的相互作用$x_i\tilde{x}_j$，然后以一种内存高效的方式隐含地将它们投射到$d$维。然而，直接的方法有一个立方级别的成本。

我们的交叉层提供了一个有效的解决方案，将成本降低到线性维度d。考虑$X_p=X_0\tilde{X}^TW$。这实际上等同于：

其中，行向量包含所有$d^2$个成对相互作用的$x_ix_j$，投影矩阵具有块对角线结构，$W∈\mathbb{R}^d$是一个列向量。

实验结果

在这一节中，我们评估了DCN在一些流行的分类数据集上的性能。

Criteo广告数据集

Criteo Display Ads数据集的目的是预测广告的点击率。它有13个整数特征和26个类别特征，每个类别都有很高的基数。对于这个数据集，0.001的logloss的改进被认为是实际意义的。当考虑到一个庞大的用户群时，预测准确性的小幅提高有可能导致公司收入的大幅增长。该数据包含11GB的用户日志，为期7天（4100万条记录）。我们使用前6天的数据进行训练，并将第7天的数据随机分成大小相同的验证集和测试集。

实现细节

DCN是在TensorFlow上实现的，我们简单讨论一下用DCN训练的一些实现细节。

关于数据处理和嵌入。实值特征通过应用对数变换进行标准化。对于分类特征，我们将这些特征嵌入到维数为6×（类别基数）1/4的密集向量中，将所有嵌入的特征串联起来，得到一个维数为1026的向量。

关于优化器。我们用Adam优化器[9]进行小批量的随机优化。批量大小被设置为512。批量归一化[6]被应用于深度网络，梯度裁剪规范被设置为100。

关于正则化。我们使用提前停止机制，因为我们没有发现L2正则化或Dropout的效果。

关于超参数。我们报告的结果是基于对隐藏层数量、隐藏层大小、初始学习率和交叉层数量的网格搜索。隐层的数量从2到5不等，隐层大小从32到1024。对于DCN，交叉层的数量从1到6。初始学习率从0.0001到0.001进行调整，增量为0.0001。所有的实验都在训练步骤150,000处采用了提前停止，超过这个步骤就开始出现过度拟合的情况。

模型对比

我们将DCN与五种模型进行比较：无交叉网络的DCN模型（DNN）、逻辑回归（LR）、因子分解机（FMs）、Wide & Deep（W&D）和Deep Cross（DC）。DNN的嵌入层、输出层和超参数调整过程与DCN相同。与DCN模型相比，唯一的变化是没有交叉层。

关于逻辑回归模型。我们使用了Sibyl[2]--一个用于分布式逻辑回归的大规模机器学习系统。整数特征在对数尺度上被离散化。交叉特征是由一个复杂的特征选择工具选择的。所有的单一特征都被使用。

关于因子分解机。我们使用了一个基于FM的有专有的细节的模型。

关于W&D。与DCN不同的是，它的Wide部分将原始稀疏特征作为输入，并依靠详尽的搜索和领域知识来选择预测的交叉特征。我们跳过了这个比较，因为目前还没有好的方法来选择交叉特征。

关于DC。与DCN相比，DC没有形成明确的交叉特征。它主要依靠堆叠和残差单元来创建隐性交叉。我们应用了与DCN相同的嵌入（堆叠）层，然后是另一个ReLu层，以产生对残差单元序列的输入。剩余单元的数量被调整为1到5，输入维度和交叉维度为100到1026。

模型性能

在这一节中，我们首先列出了不同模型在对数损失方面的最佳表现，然后我们详细比较了DCN和DNN，也就是说，我们进一步研究了交叉网络所带来的影响。

关于不同模型的性能。不同模型的最佳测试对数损失列于表1。最佳超参数设置为：DCN模型有2个1024大小的深度神经网络层和6个交叉层，DNN有5个1024大小的深度神经网络层，DC有5个输入维度为424、交叉维度为537的剩余单元，LR模型有42个交叉特征。在最深的交叉结构中发现了最佳性能，这表明来自交叉网络的高阶特征互动是有价值的。正如我们所看到的，DCN在很大程度上优于其他所有的模型。特别是，它超过了最先进的DNN模型，但只使用了DNN所消耗内存的40%。

对于每个模型的最佳超参数设置，我们还报告了10次独立运行中测试logloss的平均值和标准偏差。DCN：$0.4422±9×10^{-5}$，Dnn：$0.4430±3.7×10^{-4}$，DC：$0.4430±4.3×10^{-4}$。可以看出，DCN始终比其他模型要好很多

DCN和DNN之间的比较。考虑到交叉网络只引入了$O(d)$个额外的参数，我们将DCN与它的深度网络--传统的DNN进行比较，并在改变内存预算和损失容忍度的情况下提出实验结果。

在下文中，一定数量的参数的损失被报告为所有学习率和模型结构中的最佳验证损失。嵌入层的参数数在我们的计算中被省略，因为它对两个模型都是相同的。

表2报告了为达到理想的对数损失阈值所需的最小参数数。 从表2中，我们看到DCN比单一DNN的内存效率高近一个数量级，这要归功于交叉网络能够更有效地学习有限阶数的特征交叉。

表3比较了固定内存预算下的神经模型的性能。我们可以看到，DCN一直优于DNN。在小参数体系中，交叉网络的参数数与深度网络的参数数相当，明显的改进表明交叉网络在学习有效的特征交互方面更有效率。在大参数体系中，DNN缩小了一些差距；但是，DCN仍然比DNN高出很多，这表明它可以有效地学习某些类型的有意义的特征交互，这即使是巨大的DNN模型也无法做到。

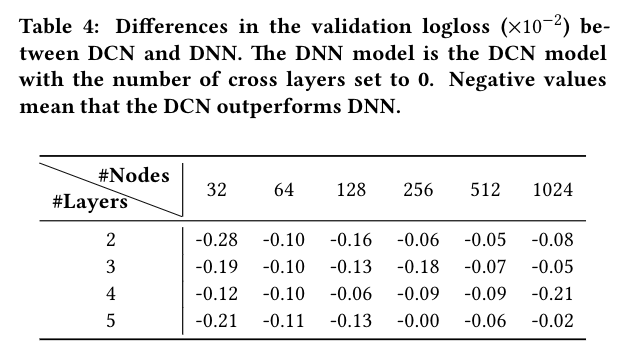
我们通过说明在给定的DNN模型中引入交叉网络的效果来更详细地分析DCN。我们首先比较了DNN和DCN在相同层数和层大小下的最佳性能，然后对于每个设置，我们展示了验证logloss是如何随着更多的交叉层的加入而变化。表4显示了DCN和DNN模型在logloss上的差异。在相同的实验环境下，DCN模型的最佳logloss一直优于相同结构的单一DNN模型。在所有的超参数中，改进是一致的，减轻了初始化和随机优化的随机性影响。

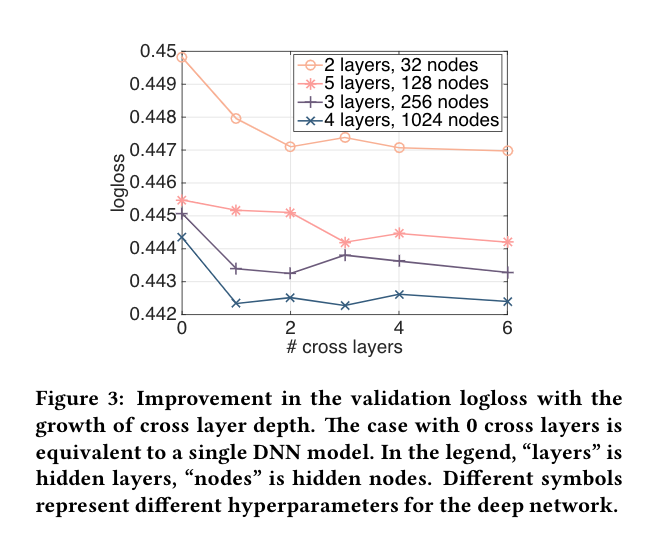
图3显示了当我们在随机选择的设置上增加交叉层的数量时的改进。对于图3中的深度神经网络，当1个交叉层被添加到模型中时，有一个明显的改善。随着更多交叉层的引入，在某些情况下，logloss持续下降，表明引入的交叉项在预测中是有效的；而在其他情况下，logloss开始波动，甚至略有增加，这表明引入的高阶特征交互并没有帮助。

非CTR数据集

我们表明，DCN在非CTR预测问题上表现良好。我们使用了UCI数据库中的森林覆盖类型（581012个样本和54个特征）和Higgs（1100万个样本和28个特征）数据集。这些数据集被随机分成训练集（90%）和测试集（10%）。对超参数进行了网格搜索。深度神经网络层的数量从1到10不等，层的大小从50到300。交叉层的数量从4到10。残差单元的数量从1到5不等，其输入维度和交叉维度从50到300不等。对于DCN，输入向量被直接送入交叉网络。

对于森林覆盖类型的数据，DCN以最小的内存消耗达到了最佳的测试精度0.9740。DNN和DC都达到了0.9737。最佳的超参数设置是：DCN有8个大小为54的交叉层和6个大小为292的深度层，DNN有7个大小为292的深度神经网络层，DC有4个输入维度为271、交叉维度为287的残差单元。

对于Higgs数据，DCN取得了最佳测试对数0.4494，而DNN取得了0.4506。最佳超参数设置为：DCN的4个交叉层大小为28，4个深度神经网络层大小为209，DNN的10个深度层大小为196。DCN的性能优于DNN，而DNN所用的内存只有一半。

结论与未来方向

识别有效的特征互动一直是许多预测模型成功的关键。遗憾的是，这个过程往往需要手工制作特征并进行详尽的搜索。DNNs在自动特征学习方面很受欢迎；然而，学到的特征是隐性的和高度非线性的，在学习某些特征时网络可能是不必要的庞大和低效的。本文提出的深层交叉网络可以处理大量的稀疏和密集特征，并与传统的深层表征共同学习阶数有限的显式交叉特征，交叉特征的程度在随着每个交叉层增加一阶。

我们希望进一步探索在其他模型中使用交叉层作为构建模块，使更深层次的交叉网络得到有效的训练，研究交叉网络在多项式近似中的效率，并更好地理解其在优化过程中与深度网络的互动。

引用

[1] Mathieu Blondel, Akinori Fujino, Naonori Ueda, and Masakazu Ishihata. 2016.Higher-Order Factorization Machines. InAdvances in Neural Information Pro-cessing Systems. 3351–3359.

[2] K. Canini. 2012. Sibyl: A system for large scale supervised machine learning.Technical Talk(2012).

[3] Olivier Chapelle, Eren Manavoglu, and Romer Rosales. 2015. Simple and scal-able response prediction for display advertising.ACM Transactions on IntelligentSystems and Technology (TIST)5, 4 (2015), 61.

[4] Heng-Tze Cheng, Levent Koc, Jeremiah Harmsen, Tal Shaked, Tushar Chandra,Hrishi Aradhye, Glen Anderson, Greg Corrado, Wei Chai, Mustafa Ispir, andothers. 2016. Wide & Deep Learning for Recommender Systems.arXiv preprintarXiv:1606.07792(2016).

[5] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2015. Deep residuallearning for image recognition.arXiv preprint arXiv:1512.03385(2015).

[6] Sergey Ioffe and Christian Szegedy. 2015. Batch normalization: Acceleratingdeep network training by reducing internal covariate shi‰.arXiv preprintarXiv:1502.03167(2015).

[7] Yuchin Juan, Damien Lefortier, and Olivier Chapelle. 2017. Field-aware factor-ization machines in a real-world online advertising system. InProceedings ofthe 26th International Conference on World Wide Web Companion. InternationalWorld Wide Web Conferences Steering CommiŠee, 680–688.

[8] Yuchin Juan, Yong Zhuang, Wei-Sheng Chin, and Chih-Jen Lin. 2016. Field-aware factorization machines for CTR prediction. InProceedings of the 10th ACMConference on Recommender Systems. ACM, 43–50.

[9] Diederik Kingma and Jimmy Ba. 2014. Adam: A method for stochastic optimiza-tion.arXiv preprint arXiv:1412.6980(2014).

[10] Yann LeCun, Yoshua Bengio, and Geoffrey Hinton. 2015. Deep learning.Nature521, 7553 (2015), 436–444.

[11] Steffen Rendle. 2010. Factorization machines. In2010 IEEE International Confer-ence on Data Mining. IEEE, 995–1000.

[12] Steffen Rendle. 2012. Factorization Machines with libFM.ACM Trans. Intell. Syst.Technol.3, 3, Article 57 (May 2012), 22 pages.

[13] Walter Rudin and others. 1964.Principles of mathematical analysis. Vol. 3.McGraw-Hill New York.

[14] J ̈urgen Schmidhuber. 2015. Deep learning in neural networks: An overview.Neural networks61 (2015), 85–117.[15] Ying Shan, T Ryan Hoens, Jian Jiao, Haijing Wang, Dong Yu, and JC Mao. 2016.Deep Crossing: Web-Scale Modeling without Manually Cra‰edCombinatorialFeatures. InProceedings of the 22nd ACM SIGKDD International ConferenceonKnowledge Discovery and Data Mining. ACM, 255–262.

[16] Gregory Valiant. 2014. Learning polynomials with neural networks. (2014).

[17] Andreas Veit, Michael J Wilber, and Serge Belongie. 2016. Residual NetworksBehave Like Ensembles of Relatively Shallow Networks. InAdvances in Neu-ral Information Processing Systems 29, D. D. Lee, M. Sugiyama, U. V. Luxburg,I. Guyon, and R. GarneŠ (Eds.). Curran Associates, Inc., 550–558.

[18] Jiyan Yang and Alex GiŠens. 2015. Tensor machines for learning target-specificpolynomial features.arXiv preprint arXiv:1504.0169