摘要

大规模图中节点的低维嵌入在各种预测任务中都证明非常有用，从内容推荐到鉴定蛋白质功能等。然而，大多数现有方法要求在嵌入训练期间所有图中的节点都必须存在；这些以前的方法本质上是传导性的，不会自然地泛化到未见过的节点。在这里，我们介绍了GraphSAGE，这是一个通用的归纳框架，利用节点特征信息（例如文本属性）来有效地生成以前未见数据的节点嵌入。我们不是为每个节点训练单独的嵌入，而是学习一个函数，通过从节点的本地邻域中进行采样和聚合特征来生成嵌入。我们的算法在三个归纳节点分类基准上表现优越：我们基于引用和Reddit帖子数据对不可见节点的类别进行分类，同时还展示了我们的算法如何泛化到完全未见的图，使用一个蛋白质相互作用的多图数据集。

引言

大规模图中节点的低维向量嵌入已经被证明是一种非常有用的特征输入，适用于各种预测和图分析任务[5, 11, 28, 35, 36]。节点嵌入方法背后的基本思想是使用降维技术将关于节点图邻域的高维信息提炼成一个密集的向量嵌入。然后，这些节点嵌入可以输入到下游机器学习系统中，有助于节点分类、聚类和链接预测等任务[11, 28, 35]。

然而，以往的研究主要集中在嵌入来自单一固定图的节点上，而许多实际应用需要能够快速为未见节点或全新的（子）图生成嵌入。这种归纳能力对于高吞吐量的生产机器学习系统至关重要，这些系统在不断变化的图上运行，并不断遇到未见节点（例如Reddit上的帖子、YouTube上的用户和视频）。采用归纳方法生成节点嵌入还有助于在具有相同特征形式的图之间进行泛化，例如，可以在从一个模型生物体中派生的蛋白质相互作用图上训练一个嵌入生成器，然后使用训练好的模型轻松为新生物体收集的数据生成节点嵌入。

归纳节点嵌入问题相对于传导性设置来说特别困难，因为要将新观察到的子图泛化到未见节点，需要将其与算法已经优化的节点嵌入进行“对齐”。一个归纳框架必须学会识别节点邻域的结构特性，这些特性既揭示了节点在图中的局部角色，也反映了其全局位置。

大多数现有的生成节点嵌入的方法本质上是传导性的。这些方法中的大多数都直接使用基于矩阵分解的目标函数来优化每个节点的嵌入，因为它们对单一、固定的图中的节点进行预测，所以不会自然地泛化到未见数据[5, 11, 23, 28, 35, 36, 37, 39]。虽然这些方法可以被修改以在归纳性设置中运行（例如，[28]），但这些修改往往计算成本高昂，需要额外的梯度下降轮次，才能进行新的预测。最近也有一些使用卷积操作来学习图结构的方法，这些方法作为一种嵌入方法具有潜力[17]。到目前为止，图卷积网络（GCNs）只在具有固定图的传导性设置中应用[17, 18]。在这项工作中，我们将GCNs扩展到归纳无监督学习任务，并提出了一个框架，将GCN方法泛化为使用可训练的聚合函数（而不仅仅是简单的卷积）。

在本研究中，我们提出了一个名为GraphSAGE（SAmple and aggreGatE）的通用框架，用于归纳性节点嵌入。与基于矩阵分解的嵌入方法不同，我们利用节点特征（例如文本属性、节点配置信息、节点度数）来学习一个嵌入函数，以便泛化到未见节点。通过将节点特征纳入学习算法中，我们同时学习了每个节点邻域的拓扑结构以及邻域中节点特征的分布。尽管我们关注的是具有丰富特征的图（例如带有文本属性的引用数据、带有功能/分子标记的生物数据），但我们的方法也可以利用所有图中存在的结构特征（例如节点度数）。因此，我们的算法也可以应用于没有节点特征的图。

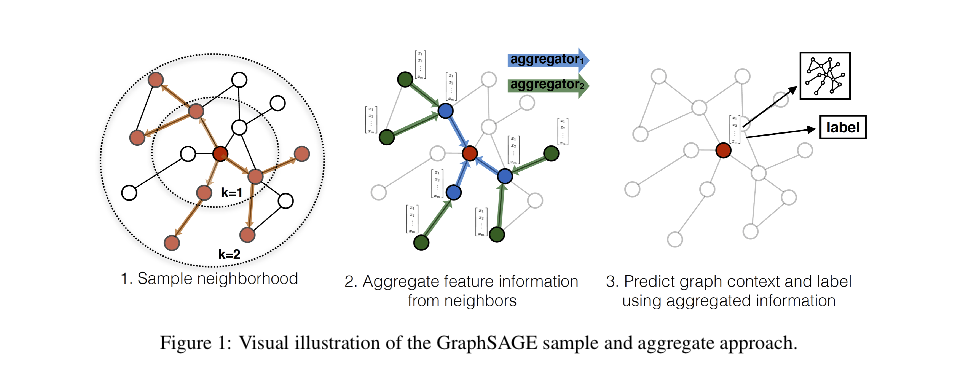
与为每个节点训练一个不同的嵌入向量不同，我们训练一组聚合函数，这些函数学会从节点的本地邻域中聚合特征信息（见图1）。每个聚合函数从距离给定节点不同数量的跳数或搜索深度处聚合信息。在测试或推断时，我们使用我们训练好的系统，通过应用学到的聚合函数来为完全未见的节点生成嵌入。遵循以前关于生成节点嵌入的工作，我们设计了一个无监督的损失函数，允许GraphSAGE在没有特定任务监督的情况下进行训练。我们还展示了GraphSAGE可以以完全监督的方式进行训练。

我们在三个节点分类基准上评估了我们的算法，这些基准测试了GraphSAGE在未见数据上生成有用嵌入的能力。我们使用了两个基于引用数据和Reddit帖子数据的不断演化的文档图（分别预测论文和帖子的类别），以及一个基于蛋白质相互作用数据集的多图泛化实验（预测蛋白质功能）。通过这些基准，我们展示了我们的方法能够有效地生成未见节点的表示，并且在各个领域中，相对于仅使用节点特征，我们的监督方法将分类F1分数平均提高了51%，GraphSAGE始终表现出色，优于强有力的传导性基线[28]，尽管该基线在未见节点上运行时间约为∼100倍。我们还展示了我们提出的新的聚合器架构相对于受到图卷积网络启发的聚合器提供了显著的增益（平均增益7.4%）。最后，我们通过理论分析探讨了我们方法的表达能力，并展示了GraphSAGE能够学习有关节点在图中角色的结构信息，尽管它本质上是基于特征的（第5节）。

相关工作

我们的算法在概念上与先前的节点嵌入方法、用于在图上学习的通用监督方法以及最近在将卷积神经网络应用于图结构数据方面的进展相关

基于因子分解的嵌入方法：有许多最近的节点嵌入方法使用随机游走统计和基于矩阵因子分解的学习目标来学习低维嵌入[5, 11, 28, 35, 36]。这些方法还与更经典的谱聚类方法[23]、多维缩放方法[19]以及PageRank算法[25]有密切关系。由于这些嵌入算法直接训练单个节点的节点嵌入，它们本质上是传导性的，至少需要昂贵的额外训练（例如通过随机梯度下降）才能对新节点进行预测。此外，对于许多这些方法（例如[11, 28, 35, 36]），目标函数对于嵌入的正交变换是不变的，这意味着嵌入空间不会在不同图之间自然泛化，并且在重新训练过程中可能会漂移。这一趋势的一个显著例外是Yang等人引入的Planetoid-I算法[40]，它是一种归纳的、基于嵌入的半监督学习方法。然而，Planetoid-I在推断过程中不使用任何图结构信息；相反，在训练期间将图结构用作正则化的一种形式。与这些以前的方法不同，我们利用特征信息来训练模型，以便为未见节点生成嵌入。

在图结构数据上的监督学习：除了节点嵌入方法之外，还有丰富的文献关于在图结构数据上进行监督学习。这包括各种基于核函数的方法，其中用于图的特征向量是从不同的图核中派生出来的（请参考[32]及其中的参考文献）。最近还出现了许多关于在图结构上进行监督学习的神经网络方法[7, 10, 21, 31]。我们的方法在概念上受到这些算法的启发。然而，与这些以前的方法试图对整个图（或子图）进行分类不同，本研究的重点是为个别节点生成有用的表示。

图卷积网络：近年来，已经提出了几种用于在图上进行学习的卷积神经网络架构（例如[4, 9, 8, 17, 24]）。这些方法中的大多数不适用于大型图，或者是为整个图分类（或两者兼顾）而设计的[4, 9, 8, 24]。然而，我们的方法与图卷积网络（GCN）密切相关，GCN由Kipf等人引入[17, 18]。最初的GCN算法[17]设计用于传导性设置下的半监督学习，确切的算法要求在训练期间知道完整的图拉普拉斯矩阵。我们的算法的一个简单变种可以看作是将GCN框架扩展到归纳性设置的一种方法，这一点我们将在第3.3节中重新讨论。

Proposed method: GraphSAGE

我们方法的关键思想是学习如何从节点的本地邻域聚合特征信息（例如，附近节点的度数或文本属性）。首先，我们描述了GraphSAGE嵌入生成（即前向传播）算法，该算法生成节点的嵌入，假设GraphSAGE模型参数已经学习（第3.1节）。然后，我们描述了如何使用标准的随机梯度下降和反向传播技术来学习GraphSAGE模型参数（第3.2节）。

Embedding generation (i.e., forward propagation) algorithm

在本节中，我们描述了嵌入生成或前向传播算法（算法1），该算法假定模型已经被训练，并且参数已固定。具体来说，我们假设已经学习了$K$个聚合器函数的参数（表示为 AGGREGATE $_{k}, \forall k \in\{1, \ldots, K\}$），这些函数用于聚合来自节点邻居的信息，以及一组权重矩阵 $\mathbf{W}^{k}, \forall k \in\{1, \ldots, K\}$，用于在模型的不同层或“搜索深度”之间传播信息。第3.2节描述了我们如何训练这些参数。

算法1背后的直觉是，在每次迭代或搜索深度中，节点从其本地邻居那里聚合信息，随着这个过程的迭代，节点逐渐从图的更远处获得更多信息。

Algorithm 1描述了在整个图$\mathcal{G}=(\mathcal{V}, \mathcal{E})$和所有节点$\mathbf{x}_{v}, \forall v \in \mathcal{V}$的特征都作为输入提供的情况下，嵌入生成过程。我们将如何将其推广到小批量设置描述如下。算法1外循环中的每一步都按以下方式进行，其中$k$表示外循环中的当前步骤（或搜索的深度），$\mathbf{h}^{k}$表示节点在这一步的表示：首先，每个节点$v \in \mathcal{V}$将其直接邻居节点的表示$\left\{\mathbf{h}_{u}^{k-1}, \forall u \in \mathcal{N}(v)\right\}$聚合成一个单一向量$\mathbf{h}_{\mathcal{N}(v)}^{k-1}$。需要注意的是，这个聚合步骤依赖于前一次外循环（即$k-1$）生成的表示，而$k=0$（“基础情况”）的表示被定义为输入节点特征。在聚合相邻特征向量之后，GraphSAGE然后将节点的当前表示$\mathbf{h}_{v}^{k-1}$与聚合的邻域向量$\mathbf{h}_{\mathcal{N}(v)}^{k-1}$进行串联，并将这个串联向量通过具有非线性激活函数$\sigma$的全连接层传递，将表示转换为下一步算法中要使用的表示（即$\mathbf{h}_{v}^{k}, \forall v \in \mathcal{V}$）。为了方便表示，我们将在深度$K$输出的最终表示表示为$\mathbf{z}_{v} \equiv \mathbf{h}_{v}^{K}, \forall v \in \mathcal{V}$。邻居表示的聚合可以由多种聚合器架构完成（在算法1中用AGGREGATE占位符表示），我们将在下面的第3.3节讨论不同的架构选择。

要将算法1扩展到小批量设置中，给定一组输入节点，我们首先前向采样所需的邻域集合（深度最多为$K$），然后运行内循环（算法11中的第3行），但不是迭代所有节点，而是仅计算每个深度满足递归所需的表示（附录A包含完整的小批量伪代码）。

与Weisfeiler-Lehman同构性测试的关系：GraphSAGE算法在概念上受到了用于测试图同构性的经典算法的启发。如果在算法1中，我们（i）将$K=|\mathcal{V}|$，（ii）将权重矩阵设置为单位矩阵，并且（iii）使用适当的哈希函数作为聚合器（没有非线性），那么算法1就是Weisfeiler-Lehman（WL）同构性测试的一个实例，也称为“朴素顶点细化”[32]。如果算法1为两个子图输出的表示集合$\left\{\mathbf{z}_{v}, \forall v \in \mathcal{V}\right\}$是相同的，那么WL测试会宣布这两个子图是同构的。已知这种测试在某些情况下会失败，但对于广泛的图类是有效的[32]。GraphSAGE是对WL测试的一个连续近似，其中我们将哈希函数替换为可训练的神经网络聚合器。当然，我们使用GraphSAGE生成有用的节点表示，而不是用于测试图同构性。然而，GraphSAGE与经典的WL测试之间的联系为我们的算法设计提供了理论背景，可以学习节点邻域的拓扑结构。

单射函数，输入不同结构得到不同表示

邻域定义：在这项工作中，我们均匀地从固定大小的邻居集合中抽样，而不是在算法1中使用完整的邻居集合，以便保持每个批次的计算开销固定${ }^{3}$。也就是说，使用重载的符号，我们将$\mathcal{N}(v)$定义为从集合$\{u \in \mathcal{V}:(u, v) \in \mathcal{E}\}$中均匀抽样得到的固定大小集合，并且在算法1的每次迭代$k$中抽取不同的均匀样本。如果不进行这种抽样，单个批次的内存使用和预期运行时间将是不可预测的，最坏情况下为$O(|\mathcal{V}|)$。相比之下，GraphSAGE的每批次空间和时间复杂度固定为$O\left(\prod_{i=1}^{K} S_{i}\right)$，其中$S_{i}, i \in\{1, \ldots, K\}$和$K$是用户指定的常数。实际上，我们发现我们的方法可以在$K=2$和$S_{1} \cdot S_{2} \leq 500$的情况下获得高性能（详见第4.4节）。

邻居重要性采样固定大小（如果邻居节点不够是否需要重复过采样）

Learning the parameters of GraphSAGE

为了在完全无监督的情况下学习有用的、具有预测性的表示，我们将一个基于图的损失函数应用于输出表示$\mathbf{z}_{u}, \forall u \in \mathcal{V}$，并通过随机梯度下降调整权重矩阵$\mathbf{W}^{k}, \forall k \in\{1, \ldots, K\}$和聚合器函数的参数。基于图的损失函数鼓励附近的节点具有相似的表示，同时强制不同节点的表示高度不同：

其中$v$是在固定长度的随机游走中与$u$附近共现的节点，$\sigma$是sigmoid函数，$P_{n}$是一个负采样分布，$Q$定义了负样本的数量。重要的是，与以前的嵌入方法不同，我们馈送到这个损失函数中的表示$\mathbf{z}_{u}$是从节点的本地邻域中包含的特征生成的，而不是为每个节点训练一个独特的嵌入（通过嵌入查找）。

$\mathbf{z}$属于标准化向量，点积后等价于cos相似度是一个标量，损失函数越小，鼓励样本与其邻居的相似度越大，与其负样本趋于正交

这个无监督设置模拟了节点特征被提供给下游机器学习应用程序的情况，作为一项服务或在静态存储库中。在仅用于特定下游任务的表示时，无监督损失（方程1p）可以简单地被替换或扩展为一个任务特定的目标（例如，交叉熵损失）。

Aggregator Architectures

与在N维格子上的机器学习不同（例如，句子、图像或3D体积），节点的邻居没有自然的顺序；因此，算法1中的聚合器函数必须在无序的向量集合上操作。理想情况下，聚合器函数应该是对称的（即对其输入的排列不变），同时仍然可以进行训练并保持高表示能力。聚合函数的对称性质确保了我们的神经网络模型可以对任意顺序的节点邻域特征集进行训练和应用。我们考察了三个候选的聚合器函数：

均值聚合器：我们的第一个候选聚合器函数是均值运算符，我们简单地计算$\left\{\mathbf{h}_{u}^{k-1}, \forall u \in \mathcal{N}(v)\right\}$中向量的逐元素平均值。均值聚合器几乎等同于在传统的GCN框架中使用的卷积传播规则[17]。特别地，我们可以通过用以下方式替换算法1中的第4和第5行来导出GCN方法的归纳变体：$4^{4}$

邻居并上本身逐元素取平均

我们将这个修改后的基于均值的聚合器称为卷积聚合器，因为它是局部谱卷积的一种粗糙的线性近似[17]。这个卷积聚合器与我们提出的其他聚合器之间的一个重要区别是，它不执行算法1的第5行中的串联操作，即卷积聚合器不会将节点的前一层表示$\mathbf{h}_{v}^{k-1}$与聚合的邻域向量$\mathbf{h}_{\mathcal{N}(v)}^{k}$进行串联。这个串联可以被看作是GraphSAGE算法的不同“搜索深度”或“层”之间的一种简单形式的“跳跃连接”[13]，它导致了性能的显著提高（第4节）。

LSTM聚合器：我们还考察了一种基于LSTM架构[14]的更复杂的聚合器。与均值聚合器相比，LSTM具有更大的表达能力。然而，值得注意的是，LSTM并不固有地对称（即它们不是置换不变的），因为它们按顺序处理它们的输入。我们通过简单地将LSTM应用于节点邻居的随机排列来使其适应无序集合的操作。

池化聚合器：我们考察的最后一个聚合器既是对称的又可训练的。在这个池化方法中，每个邻居的向量都通过一个独立的全连接神经网络进行处理；在这个转换之后，通过逐元素的最大池化操作来聚合邻居集合中的信息：

其中max表示逐元素的最大运算符，$\sigma$是非线性激活函数。原则上，在最大池化之前应用的函数可以是任意深度的多层感知器，但在这项工作中，我们专注于简单的单层架构。这个方法受到了将神经网络架构应用于学习一般点集的最新进展的启发[29]。直观地说，多层感知器可以被视为一组函数，用于计算邻域集合中每个节点表示的特征。通过将最大池化操作应用于每个计算出的特征，模型有效地捕获了邻域集合的不同方面。还要注意的是，原则上，可以在最大运算符的位置使用任何对称向量函数（例如，逐元素平均值）。我们在开发测试中没有发现最大池化和均值池化之间的显著差异，因此在后续的实验中专注于最大池化。

Experiments

我们在三个基准任务上测试了GraphSAGE的性能：(i) 使用Web of Science引用数据集将学术论文分类为不同的学科，(ii) 使用Reddit帖子将其分类为不同的社区，(iii) 在各种生物蛋白质-蛋白质相互作用（PPI）图中对蛋白质功能进行分类。第4.1和4.2节总结了数据集，补充材料中包含了额外的信息。在所有这些实验中，我们对在训练期间未见过的节点进行预测，并且在PPI数据集的情况下，我们在完全未见过的图上进行测试。

实验设置。为了在归纳基准上对实验结果进行上下文化，我们与四个基线进行了比较：随机分类器、忽略图结构的逻辑回归特征分类器（基于特征的分类器）、DeepWalk算法[28]作为代表性的基于因子分解的方法，以及原始特征和DeepWalk嵌入的串联。我们还比较了使用不同聚合器函数的四个GraphSAGE变体（第3.3节）。由于“卷积”变体的GraphSAGE是Kipf等人的半监督GCN[17]的扩展的归纳版本，我们将这个变体称为GraphSAGE-GCN。我们测试了根据方程（1）中的损失训练的GraphSAGE的无监督变体，以及直接根据分类交叉熵损失进行训练的有监督变体。对于所有GraphSAGE变体，我们使用修正线性单元作为非线性，并设置$K=2$，邻域样本大小为$S_{1}=25$和$S_{2}=10$（有关敏感性分析，请参见第4.4节）。

对于Reddit和引用数据集，我们使用DeepWalk的“在线”训练，如Perozzi等人[28]所述，在进行预测之前运行新一轮的SGD优化以嵌入新的测试节点（有关详细信息，请参见附录）。在多图设置中，我们无法应用DeepWalk，因为通过在不同的不相交图上运行DeepWalk算法生成的嵌入空间可以相对于彼此任意旋转（附录[D]）。

所有模型都是在TensorFlow [1]中实现的，使用Adam优化器 [16]（除了DeepWalk，后者使用普通梯度下降优化器效果更好）。我们设计了实验的目标，即(i)验证GraphSAGE相对于基线方法（即原始特征和DeepWalk）的改进，并(ii)对不同的GraphSAGE聚合器架构进行严格比较。为了提供公平的比较，所有模型共享相同的minibatch迭代器、损失函数和邻域采样器的实现（如果适用）。此外，为了防止在GraphSAGE聚合器之间的比较中意外发生“超参数滥用”，我们为所有GraphSAGE变体扫描相同的超参数集合（根据在验证集上的性能选择每个变体的最佳设置）。可能的超参数值集合是通过使用我们随后从分析中丢弃的引用和Reddit数据子集进行的早期验证测试来确定的。附录包含更多的实现细节[5]。

Inductive learning on evolving graphs: Citation and Reddit data

我们的前两个实验涉及到在不断演化的信息图中对节点进行分类的任务，这对于高吞吐量的生产系统尤其重要，因为它们不断遇到未见过的数据。

引用数据。我们的第一个任务是在一个大型引用数据集上预测论文的主题类别。我们使用了从汤姆逊路透Web of Science Core Collection中获取的无向引用图数据集，该数据集对应于2000年至2005年间六个与生物学相关的领域的所有论文。该数据集的节点标签对应于六种不同的领域标签。总共，该数据集包含了302,424个节点，平均度为9.15。我们在2000年至2004年的数据上训练所有算法，并使用2005年的数据进行测试（其中30%用于验证）。对于特征，我们使用了节点度数，并根据Arora等人的句子嵌入方法处理了论文摘要，使用了使用GenSim word2vec实现[30]训练的300维词向量。

Reddit数据。在我们的第二个任务中，我们预测不同Reddit帖子属于哪个社区。Reddit是一个大型在线讨论论坛，用户可以在不同的主题社区发布帖子和评论内容。我们构建了一个来自Reddit帖子的图数据集，这些帖子是在2014年9月份发布的。在这种情况下，节点标签是一个帖子所属的社区或“subreddit”。我们对50个大型社区进行了抽样，并构建了一个帖子到帖子的图，如果同一用户在两者上都发表评论，则连接这两个帖子。总共，该数据集包含了232,965个帖子，平均度为492。我们使用前20天进行训练，剩余的天数进行测试（其中30%用于验证）。对于特征，我们使用了现成的300维GloVe CommonCrawl词向量[27]；对于每个帖子，我们连接了（i）帖子标题的平均嵌入，（ii）所有帖子评论的平均嵌入，（iii）帖子的分数，以及（iv）帖子上的评论数。

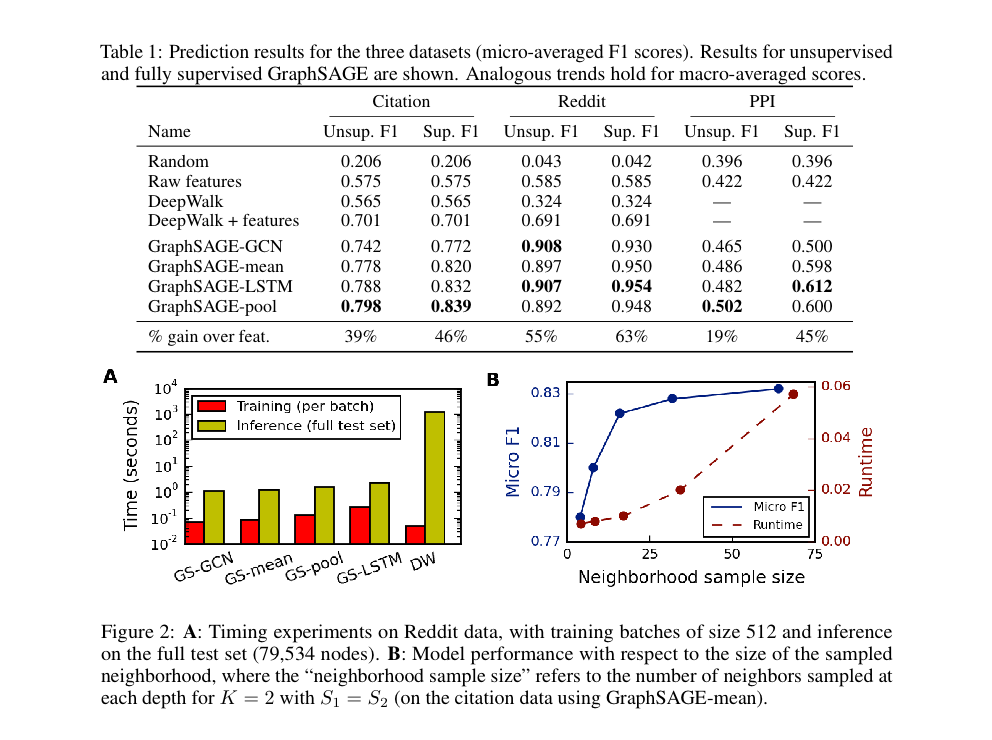
表1的前四列总结了这两个数据集上GraphSAGE以及基线方法的性能。我们发现GraphSAGE在所有基线方法上都取得了显著的优势，而可训练的神经网络聚合器相对于GCN方法提供了显著的增益。例如，无监督变体GraphSAGE-pool在引用数据上的性能优于DeepWalk嵌入和原始特征的串联，分别提高了13.8%和Reddit数据上的29.1%，而有监督版本则分别提高了19.7%和37.2%。有趣的是，尽管LSTM基础的聚合器是为序列数据而不是无序集合设计的，但它表现出了很强的性能。最后，我们发现无监督GraphSAGE的性能与完全监督版本相当竞争，这表明我们的框架可以在没有任务特定微调的情况下实现强大的性能。

Generalizing across graphs: Protein-protein interactions

现在，我们考虑跨图的任务，这需要学习节点的角色而不是社区结构。我们在不同的蛋白质-蛋白质相互作用（PPI）图中对蛋白质的细胞功能进行分类，每个图对应于不同的人体组织[41]。我们使用了从分子签名数据库[34]中收集的位置基因集、模体基因集和免疫学标志作为特征，以及基因本体集作为标签（共121个）。平均图包含2373个节点，平均度为28.8。我们在20个图上训练所有算法，然后在两个测试图上平均预测F1分数（另外两个图用于验证）。

表1的最后两列总结了这些数据上各种方法的准确性。同样，我们看到GraphSAGE明显优于基线方法，而基于LSTM和池化的聚合器相对于基于均值和GCN的聚合器提供了显著的增益。

Runtime and parameter sensitivity

图2.A总结了不同方法的训练和测试运行时间。这些方法的训练时间是可比的（其中GraphSAGE-LSTM最慢）。然而，需要对未见节点进行新的随机游走采样并运行新一轮的SGD来嵌入这些节点，使得DeepWalk在测试时变得较慢，慢了100-500倍。

对于GraphSAGE的变种，我们发现将K设置为2相对于K=1平均提高了大约10-15%的准确性；然而，将K增加到2以上的性能回报较小（0-5%），而运行时间增加了大约10-100倍，这取决于邻域样本大小。我们还发现，采样较大的邻域会产生递减的效益（图2 B）。因此，尽管子采样邻域引入了更高的方差，但GraphSAGE仍然能够保持强大的预测准确性，同时显著提高了运行时间。

Summary comparison between the different aggregator architectures

总体而言，我们发现基于LSTM和池化的聚合器在平均性能和它们是最佳方法的实验设置数量方面表现最好（表11）。为了更多定量洞察这些趋势，我们将每个六种不同的实验设置（即（3个数据集）×（无监督与有监督））视为试验，并考虑哪些性能趋势可能是普遍的。具体来说，我们使用非参数的Wilcoxon符号秩检验来量化不同聚合器在试验之间的差异，报告适用时的T-统计量和p值。请注意，这种方法是基于排名的，本质上是测试我们是否期望在新的实验设置中一种特定方法会胜过另一种方法。鉴于我们只有6种不同设置的小样本量，这种显著性检验可能有些不足；尽管如此，T-统计和相关的p值是用来评估聚合器相对性能的有用定量指标。

我们可以看到，基于LSTM、池化和均值的聚合器都比基于GCN的方法提供了统计显著的收益（对于所有三种方法，T=1.0，p=0.02）。然而，LSTM和池化方法相对于均值聚合器的收益较小（比较LSTM和均值时，T=1.5，p=0.03；比较池化和均值时，T=4.5，p=0.10）。LSTM和池化方法之间没有显著差异（T=10.0，p=0.46）。然而，GraphSAGE-LSTM比GraphSAGE-pool明显慢（大约2倍），这可能在总体上给了基于池化的聚合器稍微优势。

结论

我们介绍了一种新颖的方法，可以有效地生成未见节点的嵌入。GraphSAGE在性能和运行时之间进行有效的权衡，一直优于最先进的基线方法，通过对节点邻域进行采样，而我们的理论分析为我们的方法如何学习局部图结构提供了洞察。还有许多扩展和潜在的改进可能性，比如扩展GraphSAGE以包含定向或多模态图。未来工作的一个特别有趣的方向是探索非均匀的邻域采样函数，甚至可能将这些函数作为GraphSAGE优化的一部分来学习。

附录

A Minibatch pseudocode

为了使用随机梯度下降，我们修改了我们的算法，以允许对节点和边的小批量进行前向和后向传播。在这里，我们关注小批量前向传播算法，类似于算法1。在GraphSAGE的前向传播中，小批量$\mathcal{B}$包含我们想要生成表示的节点。算法2提供了小批量方法的伪代码。

Algorithm 2的主要思想是首先对计算所需的所有节点进行采样。Algorithm 2的第2到7行对应于采样阶段。每个集合$\mathcal{B}^{k}$包含需要计算第$(k+1)$次迭代或“层次”（即GraphSAGE算法的第$k+1$层）的节点的表示的节点，即$\mathcal{B}^{k+1}$中的节点。第9到15行对应于聚合阶段，几乎与批量推断算法相同。请注意，在第12和13行中，集合$\mathcal{B}^{k}$中任何节点在第$k$次迭代的表示都可以计算，因为它的表示在第$k-1$次迭代中已经计算过，而在第$k-1$次迭代中采样的邻居的表示也已经计算过。因此，该算法避免计算不在当前小批处理中且不在当前随机梯度下降迭代中使用的节点的表示。我们使用符号$\mathcal{N}_{k}(u)$来表示一个确定性函数，该函数指定了节点邻域的随机采样（即假设随机性是在映射中预先计算的）。我们通过索引这个函数来表示$k$，以表示在$k$上的迭代中随机样本是独立的。我们在这项工作中使用均匀采样函数，并在样本大小大于节点度数的情况下进行有替代地采样。

请注意，Algorithm 2中的采样过程在概念上与Algorithm 1中对$k$的迭代相反。我们从“第K层”节点（即我们希望在第K层之后生成其表示的$\mathcal{B}$中的节点）开始进行邻居和节点的采样，依此类推。这导致邻域采样大小的定义可能有些反直觉。特别是，如果我们使用$K=2$个总迭代次数和采样大小$S_{1}$和$S_{2}$，那么这意味着我们在Algorithm 1的第$k=1$次迭代中采样$S_{1}$个节点，在第$k=2$次迭代中采样$S_{2}$个节点，并且从我们希望在第$k=2$次迭代之后生成其表示的“目标”节点的角度来看，这相当于采样了它们的直接邻居中的$S_{2}$个节点以及它们的2跳邻居中的$S_{1} \cdot S_{2}$个节点。