摘要
矩阵分解是一种将矩阵简化为其组成部分的方法,是工程数学中一个重要章节以及重要应用,其在推荐系统中的应用尤为突出。本文首先概述了矩阵分解的简介以及其分类,之后对于矩阵分解在推荐系统中的应用做了一些介绍,并就使用梯度下降矩阵分解进行了过程分析以及过程的数学公式化表述,并使用tensorflow进行编程实现与实验。
关键词:矩阵分解、奇异值分解、梯度下降、推荐系统、共现矩阵
简介
矩阵分解
矩阵分解(decomposition, factorization)是将一个矩阵拆解为数个矩阵的乘积的运算。这种方法可以简化更复杂的矩阵运算,使得这些运算可以在分解的矩阵上执行,而不是在原始矩阵本身上执行。它的衍生Non-negative matrix factorization也被用于降维等操作上。
常见的矩阵分解方法如下:
- 奇异值分解
- 特征分解
- LU分解
在计算机应用(数值分析,特征降维、推荐系统)中常用的矩阵分解的方法有:
- 奇异值分解
- 特征分解
- 梯度下降
推荐系统与共现矩阵
用户-item共现矩阵
对于推荐系统来说,一个很重要的数据部分是用户与推荐项目(item)之间的交互数据,例如点赞、评分、浏览、点踩等用户作用于item本身的一些行为。这些行为使得用户与item之间产生了联系,这些联系本身可以被描述成有向图的数据结构,该有向图的边行为代表着用户的行为,边往往从用户出发,将行为作用于item。当我们将用户行为数据抽象成有向图,为了在计算机中表示进而可以使用邻接矩阵表示该有向图。在邻接矩阵中,每个索引位置的值将是量化后的用户行为(例如将行为量化为评分,0代表没浏览过,1为点踩,2为点赞,3为点赞并收藏,等等)。
总的来说就是以这些用户行为数据为依据,拼接在一起可以构成用户-item的共现矩阵。
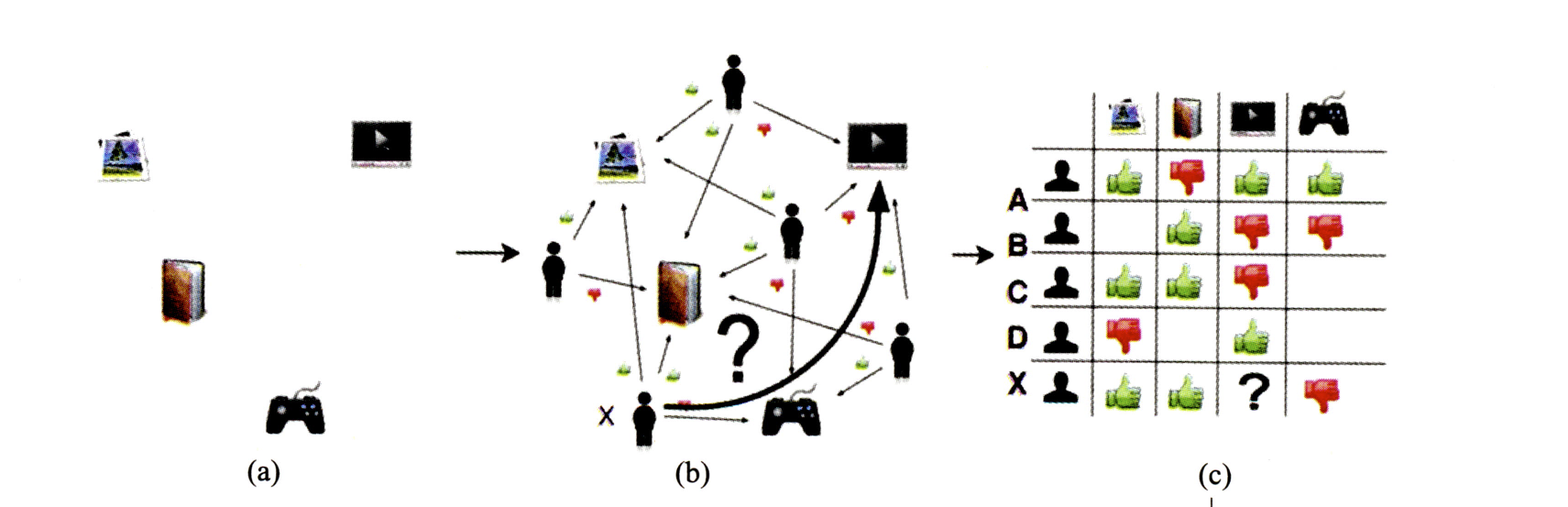
当我们构建出了用户-item共现矩阵后,如果我们将推荐系统的问题变为预测这个矩阵中所空缺的值,就引出了推荐系统中的一个经典算法族——协同过滤。
协同过滤
协同过滤的主要流程如下
- 获取用户行为数据
- 用户行为数据构建用户-item共现矩阵
- 计算用户行向量之间的相似度(其实就是把对物品的评价作为了用户embedding向量)
- 根据相似用户进行对物品的评价进行加权运算后得到该用户对于物品评价的预测分
- 针对用户推荐高预测分物品
由于协同过滤只根据共现矩阵来判断相似度,那么冷门的物品的行为更加的稀疏,缺少数据无法很好的判断相似性,就会导致头部效应(热门的物品被推荐的次数越来越多,冷门的越来越少),且只能由历史行为来判断相似性导致了对新物品的泛化能力不足。
矩阵分解
由于协同过滤存在着这些问题,隐语义模型(Latent Factor Model,LFM)受到越来越多的关注。隐语义模型最早在文本挖掘领域被提出,用于寻找文本的隐含语义,相关的模型常见的有潜在语义分析(Latent Semantic Analysis,LSA)、LDA(Latent Dirichlet Allocation)的主题模型(Topic Model)、矩阵分解(Matrix Factorization)等等。
其中矩阵分解技术是实现隐语义模型使用最广泛的一种方法,其思想也正来源于此,Yehuda Koren凭借矩阵分解模型勇夺Netflix Prize推荐比赛冠军,以矩阵分解为基础,Yehuda Koren在数据挖掘和机器学习相关的国际顶级会议(SIGIR,SIGKDD,RecSys等)发表了很多文章,将矩阵分解模型的优势发挥得淋漓尽致。实验结果表明,在个性化推荐中使用矩阵分解模型要明显优于传统的基于邻域的协同过滤(又称基于领域的协同过滤)方法,如UserCF、ItemCF等,这也使得矩阵分解成为了目前个性化推荐研究领域中的主流模型。
模型
矩阵分解与推荐系统
在推荐系统中,我们将矩阵分解应用于用户-item的共现矩阵中。假设有一共现矩阵
其中
将
也就是说我们将用户矩阵
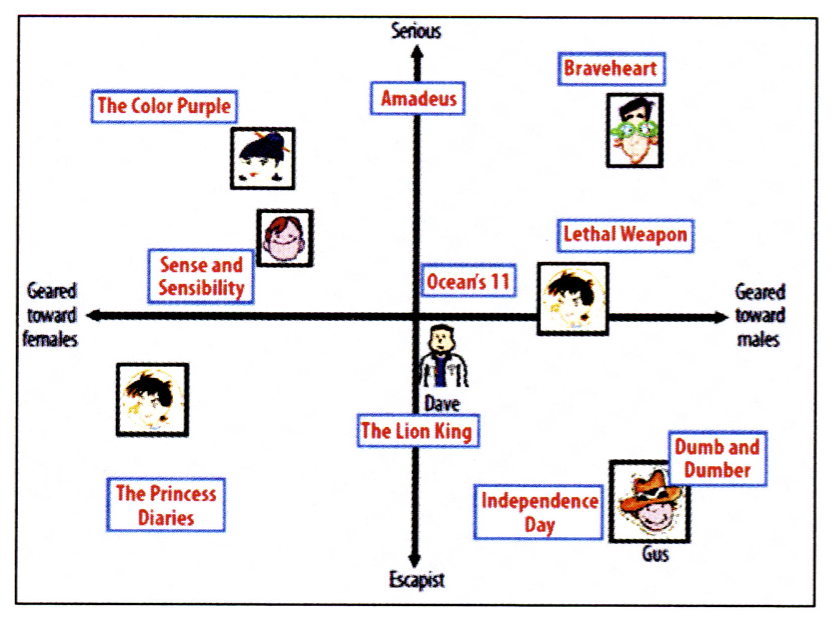
矩阵分解的求解过程
对矩阵进行矩阵分解的主要方法有三种:特征值分解( Eigen Decomposition )、 奇异值分解( Singular Value Decomposition,SVD )和梯度下降 (Gradient Deseent)。其中,特征值分解只能作用于方阵,显然不适用于分解用户-item矩阵。
对于奇异值分解来说,存在两点缺陷, 使其不宜作为互联网场景下矩阵分解的主要方法:
(1)奇异值分解要求原始的矩阵是稠密的。互联网场景下大部分用户的行为历史非常少,且由于长尾效应,有百分二十的行为将作用于很大一部分的冷门item,且这些行为分布及其稀疏,这导致了用户-item的共现矩阵非常稀疏且庞大。如果应用奇异值分解,就必须对缺失的元素值进行填充,而对于元素进行填充将会导致数据分布的改变。
(2)传统奇异值分解的计算复杂度达到了
梯度下降矩阵分解
梯度下降分解过程
梯度下降法(Gradient descent)是一个一阶最优化算法,通常也称为最陡下降法。要使用梯度下降首先需要有一个准备对其优化的函数,即损失函数,损失函数要能量化模型性能的优劣,即预测值与groud truth的差距。最优化算法的目标是将损失函数最小化,一个目标函数通常为一个损失函数的本身或者为其负值。当一个目标函数为损失函数的负值时,目标函数的值寻求最大化。
使用梯度下降进行矩阵分解的损失函数(均方误差损失MSE,加入
防止过拟合,将其加入L2正则化后:
拟合目标为:
进行梯度下降时,单个向量的梯度为:
单次参数迭代,其中
通过多次的参数迭代我们最终可以得到精度足够的用户矩阵
实验
梯度下降分解tensorflow2实现
使用movie lens数据集,由于对评分进行了归一化,模型输出需要加上sigmoid激活函数
import pandas as pd
import tensorflow as tf
from matplotlib import pyplot as plt
def build_groud_truth_matrix(rating_path='/Volumes/Data/oysterqaq/Downloads/ml-1m/ratings.dat',
user_path='/Volumes/Data/oysterqaq/Downloads/ml-1m/users.dat',
item_path='/Volumes/Data/oysterqaq/Downloads/ml-1m/movies.dat'):
ratings_list = [i.strip().split("::") for i in open(rating_path, 'r', encoding='ISO-8859-1').readlines()]
users_list = [i.strip().split("::") for i in open(user_path, 'r', encoding='ISO-8859-1').readlines()]
movies_list = [i.strip().split("::") for i in open(item_path, 'r', encoding='ISO-8859-1').readlines()]
ratings_df = pd.DataFrame(ratings_list, columns=['UserID', 'MovieID', 'Rating', 'Timestamp'], dtype=int)
movies_df = pd.DataFrame(movies_list, columns=['MovieID', 'Title', 'Genres'])
movies_df['MovieID'] = movies_df['MovieID'].apply(pd.to_numeric)
R_df = ratings_df.pivot(index='UserID', columns='MovieID', values='Rating').fillna(0)
# 归一化
return tf.constant(R_df.values.astype(float)) / 5
class MatrixFactorization(tf.keras.layers.Layer):
def __init__(self, k, **kwargs):
super(MatrixFactorization, self).__init__(**kwargs)
# 隐向量维度大小
self.k = k
def build(self, input_shape):
num_users, num_movies = input_shape
# 用户矩阵U
self.U = self.add_weight("U",
shape=[num_users, self.k],
dtype=tf.float32,
initializer=tf.initializers.GlorotUniform,
# L2正则
regularizer=tf.keras.regularizers.L2(0.01)
)
# 物品矩阵V
self.V = self.add_weight("V",
shape=[num_movies, self.k],
dtype=tf.float32,
initializer=tf.initializers.GlorotUniform,
regularizer=tf.keras.regularizers.L2(0.01)
)
# 用户矩阵bias
self.bu = self.add_weight("bu",
shape=[num_users],
dtype=tf.float32,
initializer=tf.initializers.Zeros)
# 物品矩阵bias
self.bv = self.add_weight("bv",
shape=[num_movies],
dtype=tf.float32,
initializer=tf.initializers.Zeros)
# 整体bias
self.bg = self.add_weight("bg",
shape=[],
dtype=tf.float32,
initializer=tf.initializers.Zeros)
def call(self, input, **kwargs):
return (tf.add(
tf.add(
tf.matmul(self.U, tf.transpose(self.V)),
tf.expand_dims(self.bu, axis=1)),
tf.expand_dims(self.bv, axis=0)) +
self.bg)
class MatrixFactorizer(tf.keras.Model):
def __init__(self, embedding_size):
super(MatrixFactorizer, self).__init__()
self.matrixFactorization = MatrixFactorization(embedding_size)
#
self.sigmoid = tf.keras.layers.Activation("sigmoid")
def call(self, input, **kwargs):
output = self.matrixFactorization(input)
output = self.sigmoid(output)
return output
def loss_fn(source, target):
mse = tf.keras.losses.MeanSquaredError()
loss = mse(source, target)
return loss
#分解后特征空间维度大小
k = 15
#构建用户-item共现矩阵
R = build_groud_truth_matrix()
model = MatrixFactorizer(k)
model.build(input_shape=R.shape)
model.summary()
optimizer = tf.optimizers.Adam(learning_rate=1e-2)
losses, steps = [], []
for i in range(1000):
with tf.GradientTape() as tape:
Rhat = model(R)
loss = loss_fn(R, Rhat)
if i % 100 == 0:
loss_value = loss.numpy()
losses.append(loss_value)
steps.append(i)
print("step: {:d}, loss: {:.6f}".format(i, loss_value))
variables = model.trainable_variables
gradients = tape.gradient(loss, variables)
optimizer.apply_gradients(zip(gradients, variables))
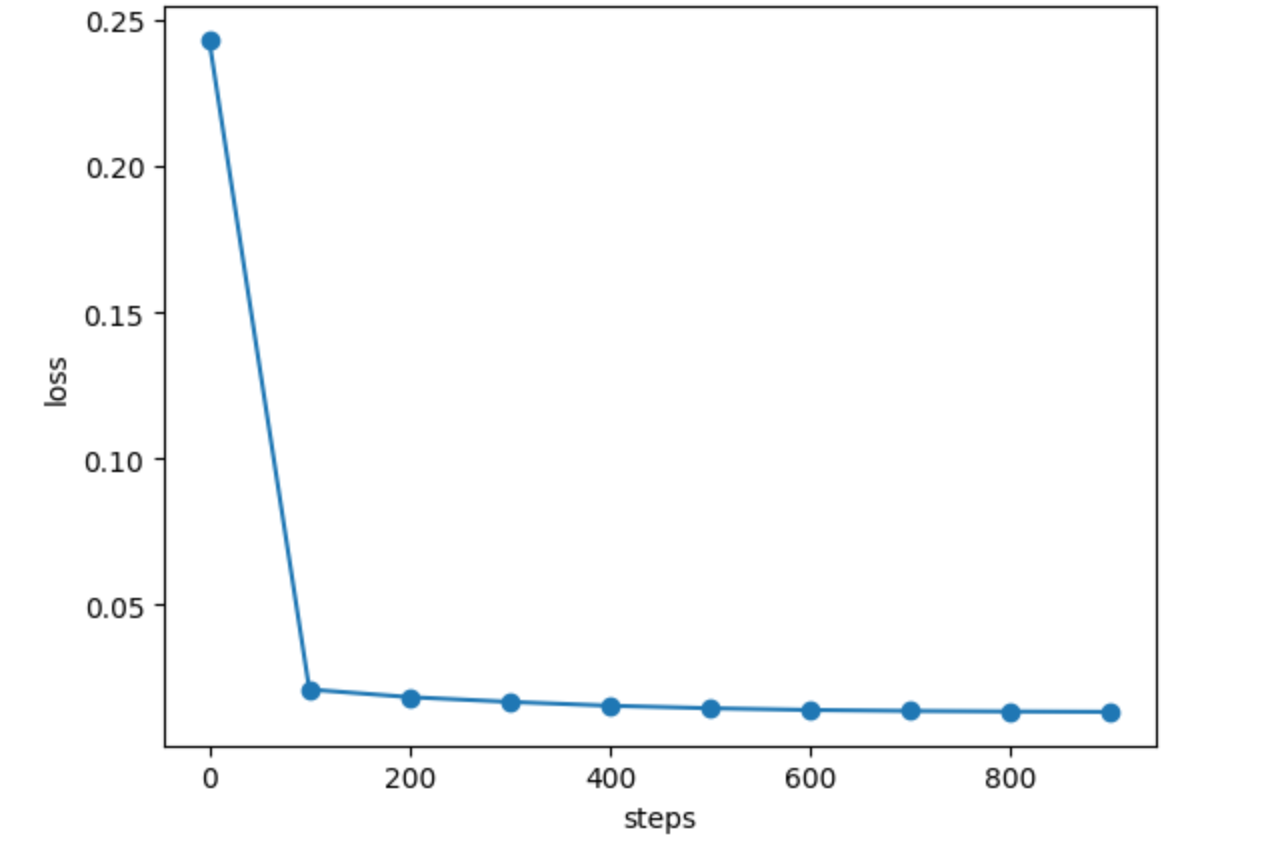
# plot training loss
plt.plot(steps, losses, marker="o")
plt.xlabel("steps")
plt.ylabel("loss")
plt.show()
结论
关于矩阵分解的个人思考
矩阵分解的变换在现实问题中代表了将用户-item共现矩阵映射到另外一个特征空间中得到一个相对密集的向量表征,将抽象成共现矩阵的用户与项目(用户与项目分别用与对方的共现关系来做一个预表征)映射到同一个特征向量空间。既然在同一个空间中那么其中向量就满足一些数学性质,并且可以计算距离,进而使用向量空间中的距离来量化用户与物品在实际物理真实世界的相关度。
参考
https://flashgene.com/archives/52522.html2022
https://zhuanlan.zhihu.com/p/399547902
《深度学习推荐系统》

Comments | NOTHING